多德-布洛-米哈伊洛夫方程(Dodd-Bullough-Mikhailov equation)是一個非線性偏微分方程[1]。

多德-布洛-米哈伊洛夫方程不是函數u的多項式形式,因此必須做代換:
 , 變為:
, 變為:

得到函數v(x,t)的行波解:








作反變換:

即得多德-布洛-米哈伊洛夫方程的行波解:










 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
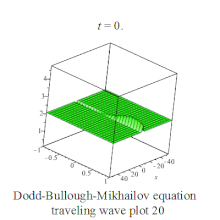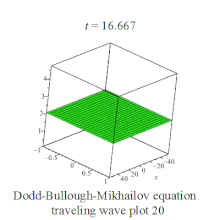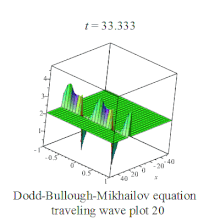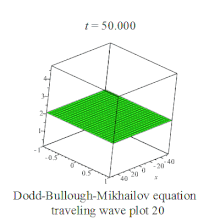 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
 Dodd-Bullough-Mikhailov equation traveling wave plot Dodd-Bullough-Mikhailov equation traveling wave plot
|
|
|
- ^ 李志斌編著 《非線性數學物理方程的行波解》 第105-107頁,科學出版社 2008
- *谷超豪 《孤立子理論中的達布變換及其幾何應用》 上海科學技術出版社
- *閻振亞著 《複雜非線性波的構造性理論及其應用》 科學出版社 2007年
- 李志斌編著 《非線性數學物理方程的行波解》 科學出版社
- 王東明著 《消去法及其應用》 科學出版社 2002
- *何青 王麗芬編著 《Maple 教程》 科學出版社 2010 ISBN 9787030177445
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759



































