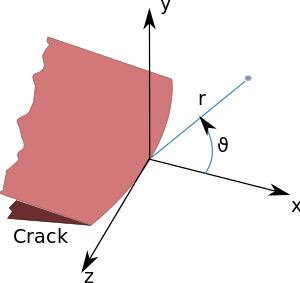
裂紋尖端的極坐標 應力強度因子 (Stress Intensity Factors),符號為K 斷裂力學 、破壞力學中極其重要的一個參量。在斷裂力學中,應力強度因子用於預測由遠程載荷或殘餘應力 引起的裂紋或凹口尖端附近的應力強度,[ 1]
K [ 2] [ 3]
K
=
σ
π
a
f
(
a
/
W
)
{\displaystyle K=\sigma {\sqrt {\pi a}}\,f(a/W)}
其中
f
(
a
/
W
)
{\displaystyle f(a/W)}
a W σ
彈性力學 理論預測,在極坐標 (
r
,
θ
{\displaystyle r,\theta }
σ
i
j
{\displaystyle \sigma _{ij}}
[ 4]
σ
i
j
(
r
,
θ
)
=
K
2
π
r
f
i
j
(
θ
)
+
h
i
g
h
e
r
o
r
d
e
r
t
e
r
m
s
{\displaystyle \sigma _{ij}(r,\theta )={\frac {K}{\sqrt {2\pi r}}}\,f_{ij}(\theta )+\,\,{\rm {higher\,order\,terms}}}
其中K 1/2 ),
f
i
j
{\displaystyle f_{ij}}
r
σ
i
j
{\displaystyle \sigma _{ij}}
∞
{\displaystyle \infty }
[ 5] r 屈服強度 的應力下,此時的線彈性解則不再適用。但如果裂尖的塑性區域相對裂紋長度很小,那麼裂尖附近的漸近應力分佈則仍然適用。
三種模式的裂紋荷載 1957年,George Rankine Irwin發現,裂紋周圍的應力可以用一個稱為應力強度因子的比例因子來表達。他發現,裂紋在任意荷載下可以分解為三種線性獨立的裂紋模式。[ 6]
對應於三種不同的斷裂模式 ,有三個不同的物理量:
K
I
{\displaystyle K_{I}}
K
I
I
{\displaystyle K_{II}}
K
I
I
I
{\displaystyle K_{III}}
[ 7]
K
I
=
lim
r
→
0
2
π
r
σ
y
y
(
r
,
0
)
K
I
I
=
lim
r
→
0
2
π
r
σ
y
x
(
r
,
0
)
K
I
I
I
=
lim
r
→
0
2
π
r
σ
y
z
(
r
,
0
)
.
{\displaystyle {\begin{aligned}K_{\rm {I}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yy}(r,0)\\K_{\rm {II}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yx}(r,0)\\K_{\rm {III}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yz}(r,0)\,.\end{aligned}}}
Equations for stress and displacement fields
在平面應力 條件下,裂紋在純I型或純II型荷載下的應變能釋放速率(
G
{\displaystyle G}
G
I
=
K
I
2
(
1
E
)
{\displaystyle G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1}{E}}\right)}
G
I
I
=
K
I
I
2
(
1
E
)
{\displaystyle G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1}{E}}\right)}
其中
E
{\displaystyle E}
楊氏模量 ,
ν
{\displaystyle \nu }
泊松比 。假設材料各向同性、分佈均勻且為線彈性,則認為裂紋會沿着初始裂紋的方向延伸。
對於平面應變 條件,等效關係為:
G
I
=
K
I
2
(
1
−
ν
2
E
)
{\displaystyle G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,}
G
I
I
=
K
I
I
2
(
1
−
ν
2
E
)
.
{\displaystyle G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,.}
對於純III型荷載為:
G
I
I
I
=
K
I
I
I
2
(
1
2
μ
)
=
K
I
I
I
2
(
1
+
ν
E
)
{\displaystyle G_{\rm {III}}=K_{\rm {III}}^{2}\left({\frac {1}{2\mu }}\right)=K_{\rm {III}}^{2}\left({\frac {1+\nu }{E}}\right)}
其中
μ
{\displaystyle \mu }
剪切模量 。對於平面應變中的一般荷載,則成立以下線性組合:
G
=
J
=
∫
Γ
(
W
d
x
2
−
t
⋅
∂
u
∂
x
1
d
s
)
.
{\displaystyle G=J=\int _{\Gamma }\left(W~dx_{2}-\mathbf {t} \cdot {\cfrac {\partial \mathbf {u} }{\partial x_{1}}}~ds\right)\,.}
與應力強度因子相對應的表徵彈塑性材料的裂紋尖端應力應變場的參量是斷裂韌性 J積分,J積分也按照斷裂模式分為
J
I
{\displaystyle J_{I}}
J
I
I
{\displaystyle J_{II}}
J
I
I
I
{\displaystyle J_{III}}
應力強度因子
K
{\displaystyle K}
Y
{\displaystyle Y}
K
I
{\displaystyle K_{\mathrm {I} }}
K
I
c
{\displaystyle K_{\mathrm {Ic} }}
K
I
c
{\displaystyle K_{\mathrm {Ic} }}
3/2 )。
K
I
c
{\displaystyle K_{\mathrm {Ic} }}
K
I
c
{\displaystyle K_{\mathrm {Ic} }}
K
I
c
{\displaystyle K_{\mathrm {Ic} }}
G準則是一種斷裂準則,它將臨界應力強度因子(或斷裂韌性)與三種模式的應力強度因子相關聯。這個失效準則可以表述為:[ 8]
K
c
2
=
K
I
2
+
K
I
I
2
+
E
′
2
μ
K
I
I
I
2
{\displaystyle K_{\rm {c}}^{2}=K_{\rm {I}}^{2}+K_{\rm {II}}^{2}+{\frac {E'}{2\mu }}\,K_{\rm {III}}^{2}}
其中,是斷裂韌性,
E
′
=
E
/
(
1
−
ν
2
)
{\displaystyle E'=E/(1-\nu ^{2})}
E
′
=
E
{\displaystyle E'=E}
K
c
{\displaystyle K_{\rm {c}}}
在I型加載下的無限大平板中的裂紋 假設長度為
2
a
{\displaystyle 2a}
σ
{\displaystyle \sigma }
[ 5] [ 7]
K
I
=
σ
π
a
{\displaystyle K_{\mathrm {I} }=\sigma {\sqrt {\pi a}}}
無限域內受單軸張力作用的硬幣形裂紋 在無限域內一個半徑為
a
{\displaystyle a}
[ 9]
K
I
=
2
π
σ
π
a
.
{\displaystyle K_{\rm {I}}={\frac {2}{\pi }}\sigma {\sqrt {\pi a}}\,.}
有限平面在I型加載下的裂縫 如果裂縫位於寬度為
2
b
{\displaystyle 2b}
2
h
{\displaystyle 2h}
[ 7]
K
I
=
σ
π
a
[
1
−
a
2
b
+
0.326
(
a
b
)
2
1
−
a
b
]
.
{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{\sqrt {1-{\frac {a}{b}}}}}\right]\,.}
如果裂紋不位於寬度的中心位置,即
d
≠
b
{\displaystyle d\neq b}
A 處的應力強度因子可以通過級數展開來近似得到:[ 7] [ 10]
K
I
A
=
σ
π
a
[
1
+
∑
n
=
2
M
C
n
(
a
b
)
n
]
{\displaystyle K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\left[1+\sum _{n=2}^{M}C_{n}\left({\frac {a}{b}}\right)^{n}\right]}
從應力強度曲線的擬合中可以基於不同
d
{\displaystyle d}
C
n
{\displaystyle C_{n}}
[ 7] B 點可以得到一個類似(但不完全相同)的表達式。在A點和B點的應力強度因子的替代表達式是:[ 11]
K
I
A
=
σ
π
a
Φ
A
,
K
I
B
=
σ
π
a
Φ
B
{\displaystyle K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\,\Phi _{A}\,\,,K_{\rm {IB}}=\sigma {\sqrt {\pi a}}\,\Phi _{B}}
其中
Φ
A
:=
[
β
+
(
1
−
β
4
)
(
1
+
1
4
sec
α
A
)
2
]
sec
α
A
Φ
B
:=
1
+
[
sec
α
A
B
−
1
1
+
0.21
sin
{
8
tan
−
1
[
(
α
A
−
α
B
α
A
+
α
B
)
0.9
]
}
]
{\displaystyle {\begin{aligned}\Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{AB}}}-1}{1+0.21\sin \left\{8\,\tan ^{-1}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{0.9}\right]\right\}}}\right]\end{aligned}}}
其中
β
:=
sin
(
π
α
B
α
A
+
α
B
)
,
α
A
:=
π
a
2
d
,
α
B
:=
π
a
4
b
−
2
d
;
α
A
B
:=
4
7
α
A
+
3
7
α
B
.
{\displaystyle \beta :=\sin \left({\frac {\pi \alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)~,~~\alpha _{A}:={\frac {\pi a}{2d}}~,~~\alpha _{B}:={\frac {\pi a}{4b-2d}}~;~~\alpha _{AB}:={\frac {4}{7}}\,\alpha _{A}+{\frac {3}{7}}\,\alpha _{B}\,.}
在上述表達試中,
d
{\displaystyle d}
d
=
b
{\displaystyle d=b}
單軸應力下有限平面中的邊緣裂紋 對於一個尺寸為
2
h
×
b
{\displaystyle 2h\times b}
a
{\displaystyle a}
h
/
b
≥
0.5
{\displaystyle h/b\geq 0.5}
a
/
b
≤
0.6
{\displaystyle a/b\leq 0.6}
σ
{\displaystyle \sigma }
[ 5]
K
I
=
σ
π
a
[
1.122
−
0.231
(
a
b
)
+
10.55
(
a
b
)
2
−
21.71
(
a
b
)
3
+
30.382
(
a
b
)
4
]
.
{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[1.122-0.231\left({\frac {a}{b}}\right)+10.55\left({\frac {a}{b}}\right)^{2}-21.71\left({\frac {a}{b}}\right)^{3}+30.382\left({\frac {a}{b}}\right)^{4}\right]\,.}
對於
h
/
b
≥
1
{\displaystyle h/b\geq 1}
a
/
b
≥
0.3
{\displaystyle a/b\geq 0.3}
K
I
=
σ
π
a
[
1
+
3
a
b
2
π
a
b
(
1
−
a
b
)
3
/
2
]
.
{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\frac {1+3{\frac {a}{b}}}{2{\sqrt {\pi {\frac {a}{b}}}}\left(1-{\frac {a}{b}}\right)^{3/2}}}\right]\,.}
雙軸加載平面中的傾斜裂縫。 對於一個長度為
2
a
{\displaystyle 2a}
y
{\displaystyle y}
σ
{\displaystyle \sigma }
x
{\displaystyle x}
α
σ
{\displaystyle \alpha \sigma }
[ 7] [ 8]
K
I
=
σ
π
a
(
cos
2
β
+
α
sin
2
β
)
K
I
I
=
σ
π
a
(
1
−
α
)
sin
β
cos
β
{\displaystyle {\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {\pi a}}\left(\cos ^{2}\beta +\alpha \sin ^{2}\beta \right)\\K_{\rm {II}}&=\sigma {\sqrt {\pi a}}\left(1-\alpha \right)\sin \beta \cos \beta \end{aligned}}}
β
{\displaystyle \beta }
x
{\displaystyle x}
在局部作用力
F
x
{\displaystyle F_{x}}
F
y
{\displaystyle F_{y}}
一個尺寸為
2
h
×
2
b
{\displaystyle 2h\times 2b}
2
a
{\displaystyle 2a}
x
,
y
{\displaystyle x,y}
F
x
{\displaystyle F_{x}}
F
y
{\displaystyle F_{y}}
在平面比裂紋尺寸大,且力的位置相對靠近裂紋的情況下,即
h
≫
a
{\displaystyle h\gg a}
b
≫
a
{\displaystyle b\gg a}
x
≪
b
{\displaystyle x\ll b}
y
≪
h
{\displaystyle y\ll h}
x
=
a
{\displaystyle x=a}
F
x
{\displaystyle F_{x}}
[ 8] [ 12]
K
I
=
F
x
2
π
a
(
κ
−
1
κ
+
1
)
[
G
1
+
1
κ
−
1
H
1
]
K
I
I
=
F
x
2
π
a
[
G
2
+
1
κ
+
1
H
2
]
{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\\K_{\rm {II}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left[G_{2}+{\frac {1}{\kappa +1}}H_{2}\right]\end{aligned}}}
其中
G
1
=
1
−
Re
[
a
+
z
z
2
−
a
2
]
,
G
2
=
−
Im
[
a
+
z
z
2
−
a
2
]
H
1
=
Re
[
a
(
z
¯
−
z
)
(
z
¯
−
a
)
z
¯
2
−
a
2
]
,
H
2
=
−
Im
[
a
(
z
¯
−
z
)
(
z
¯
−
a
)
z
¯
2
−
a
2
]
{\displaystyle {\begin{aligned}G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\\H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\end{aligned}}}
z
=
x
+
i
y
{\displaystyle z=x+iy}
z
¯
=
x
−
i
y
{\displaystyle {\bar {z}}=x-iy}
κ
=
3
−
4
ν
{\displaystyle \kappa =3-4\nu }
κ
=
(
3
−
ν
)
/
(
1
+
ν
)
{\displaystyle \kappa =(3-\nu )/(1+\nu )}
ν
{\displaystyle \nu }
泊松比 。
在B端點
F
y
{\displaystyle F_{y}}
K
I
=
F
y
2
π
a
[
G
2
−
1
κ
+
1
H
2
]
K
I
I
=
−
F
y
2
π
a
(
κ
−
1
κ
+
1
)
[
G
1
−
1
κ
−
1
H
1
]
.
{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {F_{y}}{2{\sqrt {\pi a}}}}\left[G_{2}-{\frac {1}{\kappa +1}}H_{2}\right]\\K_{\rm {II}}&=-{\frac {F_{y}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}-{\frac {1}{\kappa -1}}H_{1}\right]\,.\end{aligned}}}
點A(
x
=
−
a
{\displaystyle x=-a}
(
x
,
y
)
{\displaystyle (x,y)}
F
x
{\displaystyle F_{x}}
K
I
(
−
a
;
x
,
y
)
=
−
K
I
(
a
;
−
x
,
y
)
,
K
I
I
(
−
a
;
x
,
y
)
=
K
I
I
(
a
;
−
x
,
y
)
.
{\displaystyle K_{\rm {I}}(-a;x,y)=-K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=K_{\rm {II}}(a;-x,y)\,.}
F
y
{\displaystyle F_{y}}
K
I
(
−
a
;
x
,
y
)
=
K
I
(
a
;
−
x
,
y
)
,
K
I
I
(
−
a
;
x
,
y
)
=
−
K
I
I
(
a
;
−
x
,
y
)
.
{\displaystyle K_{\rm {I}}(-a;x,y)=K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=-K_{\rm {II}}(a;-x,y)\,.}
平面裂紋荷載 如果裂紋受到位於
y
=
0
{\displaystyle y=0}
−
a
<
x
<
a
{\displaystyle -a<x<a}
F
y
{\displaystyle F_{y}}
[ 7]
K
I
=
F
y
2
π
a
a
+
x
a
−
x
,
K
I
I
=
−
F
x
2
π
a
(
κ
−
1
κ
+
1
)
.
{\displaystyle K_{\rm {I}}={\frac {F_{y}}{2{\sqrt {\pi a}}}}{\sqrt {\frac {a+x}{a-x}}}\,,\,\,K_{\rm {II}}=-{\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\,.}
如果力在
−
a
<
x
<
a
{\displaystyle -a<x<a}
K
I
=
1
2
π
a
∫
−
a
a
F
y
(
x
)
a
+
x
a
−
x
d
x
,
K
I
I
=
−
1
2
π
a
(
κ
−
1
κ
+
1
)
∫
−
a
a
F
y
(
x
)
d
x
,
.
{\displaystyle K_{\rm {I}}={\frac {1}{2{\sqrt {\pi a}}}}\int _{-a}^{a}F_{y}(x)\,{\sqrt {\frac {a+x}{a-x}}}\,{\rm {d}}x\,,\,\,K_{\rm {II}}=-{\frac {1}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\int _{-a}^{a}F_{y}(x)\,{\rm {d}}x,\,.}
如果裂紋間距遠遠大於裂紋長度(
h
≫
a
{\displaystyle h\gg a}
K
I
=
σ
π
a
{\displaystyle {\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {\pi a}}\end{aligned}}}
如果裂紋長度遠大於間距(
a
≫
h
{\displaystyle a\gg h}
K
I
=
σ
h
{\displaystyle {\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {h}}\end{aligned}}}
用於斷裂韌性測試的緊湊拉伸樣品 緊湊拉伸試樣裂紋尖端的應力強度因子為:[ 15]
K
I
=
P
B
π
W
[
16.7
(
a
W
)
1
/
2
−
104.7
(
a
W
)
3
/
2
+
369.9
(
a
W
)
5
/
2
−
573.8
(
a
W
)
7
/
2
+
360.5
(
a
W
)
9
/
2
]
{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {P}{B}}{\sqrt {\frac {\pi }{W}}}\left[16.7\left({\frac {a}{W}}\right)^{1/2}-104.7\left({\frac {a}{W}}\right)^{3/2}+369.9\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-573.8\left({\frac {a}{W}}\right)^{7/2}+360.5\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}}
其中
P
{\displaystyle P}
B
{\displaystyle B}
a
{\displaystyle a}
W
{\displaystyle W}
用於斷裂韌性測試的單邊缺口彎曲試樣(也稱為三點彎曲試樣) 單邊缺口彎曲試樣裂紋尖端的應力強度因子為:[ 15]
K
I
=
4
P
B
π
W
[
1.6
(
a
W
)
1
/
2
−
2.6
(
a
W
)
3
/
2
+
12.3
(
a
W
)
5
/
2
−
21.2
(
a
W
)
7
/
2
+
21.8
(
a
W
)
9
/
2
]
{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {4P}{B}}{\sqrt {\frac {\pi }{W}}}\left[1.6\left({\frac {a}{W}}\right)^{1/2}-2.6\left({\frac {a}{W}}\right)^{3/2}+12.3\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-21.2\left({\frac {a}{W}}\right)^{7/2}+21.8\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}}
其中
P
{\displaystyle P}
B
{\displaystyle B}
a
{\displaystyle a}
W
{\displaystyle W}
^ Anderson, T. L. Fracture mechanics: fundamentals and applications. CRC Press. 2005. ^ Soboyejo, W. O. 11.6.2 Crack Driving Force and Concept of Similitude. Mechanical properties of engineered materials . Marcel Dekker. 2003 [2024-03-28 ] . ISBN 0-8247-8900-8OCLC 300921090 存檔 於2021-05-31). ^ Janssen, M. (Michael). Fracture mechanics . Zuidema, J. (Jan), Wanhill, R. J. H. 2nd. London: Spon Press. 2004: 41. ISBN 0-203-59686-2OCLC 57491375 ^ Hiroshi Tada ; P. C. Paris ; George R. Irwin . The Stress Analysis of Cracks Handbook 3rd. American Society of Mechanical Engineers. February 2000. ^ 5.0 5.1 5.2 Liu, M.; et al. An improved semi-analytical solution for stress at round-tip notches (PDF) . Engineering Fracture Mechanics. 2015, 149 : 134–143 [2024-03-28 ] . S2CID 51902898 doi:10.1016/j.engfracmech.2015.10.004 存檔 (PDF) 於2018-07-13). ^ Suresh, S. Fatigue of Materials. Cambridge University Press. 2004. ISBN 978-0-521-57046-6 ^ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 Rooke, D. P.; Cartwright, D. J. Compendium of stress intensity factors. HMSO Ministry of Defence. Procurement Executive. 1976. ^ 8.0 8.1 8.2 Sih, G. C.; Macdonald, B., Fracture mechanics applied to engineering problems-strain energy density fracture criterion, Engineering Fracture Mechanics, 1974, 6 (2): 361–386, doi:10.1016/0013-7944(74)90033-2 ^ Anderson, T. L. Fracture mechanics: fundamentals and applications. CRC Press. 2005. ^ Isida, M., 1966, Stress intensity factors for the tension of an eccentrically cracked strip , Transactions of the ASME Applied Mechanics Section, v. 88, p.94.
^ Kathiresan, K.; Brussat, T. R.; Hsu, T. M. Advanced life analysis methods. Crack Growth Analysis Methods for Attachment Lugs. Flight Dynamics Laboratory, Air Force Wright Aeronautical Laboratories, AFSC W-P Air Force Base, Ohio. 1984. ^ Erdogan, F., On the stress distribution in plates with collinear cuts under arbitrary loads, Proceedings of the Fourth US National Congress of Applied Mechanics, 1962, 1 : 547–574 ^ Kundu, Tribikram. Fundamentals of Fracture Mechanics . 2008-01-30. ISBN 9780429110054doi:10.1201/9781439878057 ^ 范, 天佑. 紧凑拉伸试样的K_I . Chinese Science Bulletin. 1976-07-01, 21 (Z1). ISSN 0023-074X doi:10.1360/csb1976-21-z1-494 ^ 15.0 15.1 Bower, A. F. Applied mechanics of solids. CRC Press. 2009.


















































![{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{\sqrt {1-{\frac {a}{b}}}}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cc4dadb6371c8239b7ebca823e25b13d2ffeb3)

![{\displaystyle K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\left[1+\sum _{n=2}^{M}C_{n}\left({\frac {a}{b}}\right)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71eaed2d5214af8609ee2614e072a831dff9bb27)



![{\displaystyle {\begin{aligned}\Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{AB}}}-1}{1+0.21\sin \left\{8\,\tan ^{-1}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{0.9}\right]\right\}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97a81ceb7c9a5bbd82590c76afd49d6690a9c74a)





![{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[1.122-0.231\left({\frac {a}{b}}\right)+10.55\left({\frac {a}{b}}\right)^{2}-21.71\left({\frac {a}{b}}\right)^{3}+30.382\left({\frac {a}{b}}\right)^{4}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d8ceaef43b7ab34b12662c8847e580f260cb701)


![{\displaystyle K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\frac {1+3{\frac {a}{b}}}{2{\sqrt {\pi {\frac {a}{b}}}}\left(1-{\frac {a}{b}}\right)^{3/2}}}\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a0366ab9b177d5a2d15ce70349ef83e9456f1f)














![{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\\K_{\rm {II}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left[G_{2}+{\frac {1}{\kappa +1}}H_{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9df6165ba8ba56686979fe76299274dd25540945)
![{\displaystyle {\begin{aligned}G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\\H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0255e5aec3179e43fd82a04e723ef65dff683f6f)




![{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {F_{y}}{2{\sqrt {\pi a}}}}\left[G_{2}-{\frac {1}{\kappa +1}}H_{2}\right]\\K_{\rm {II}}&=-{\frac {F_{y}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}-{\frac {1}{\kappa -1}}H_{1}\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f91850cc6735cb02154d8d82ca2b502090d7a67)











![{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {P}{B}}{\sqrt {\frac {\pi }{W}}}\left[16.7\left({\frac {a}{W}}\right)^{1/2}-104.7\left({\frac {a}{W}}\right)^{3/2}+369.9\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-573.8\left({\frac {a}{W}}\right)^{7/2}+360.5\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a74d53e379ebf47cf3ea5f1a45619a1e78dcc4ad)



![{\displaystyle {\begin{aligned}K_{\rm {I}}&={\frac {4P}{B}}{\sqrt {\frac {\pi }{W}}}\left[1.6\left({\frac {a}{W}}\right)^{1/2}-2.6\left({\frac {a}{W}}\right)^{3/2}+12.3\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-21.2\left({\frac {a}{W}}\right)^{7/2}+21.8\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/466d7f6e915a160e93963497a9016099b626cae6)