施瓦茨三角形
外观
在几何学中,施瓦茨三角形(英语:Schwarz triangle)是一个球面三角形,可用于球面镶嵌,透过在其边缘反射,但是可能会重叠。他们被归类于施瓦茨1873[1]。
施瓦茨三角形除了可以定义在球面之外,也可以定义于欧几里得平面或双曲面,而做成便面镶嵌或双曲面镶嵌。在球面上的每个施瓦茨三角形定义了一个有限群,而在欧氏或双曲平面,则会定义出一个无限群。
施瓦茨三角形是由三个有理数(p q r)来代表每个顶点的角度。值n/d表示的顶角为半圆的d/n,“2”表是一个直角。若p、q、r皆为整数,则将其称为莫比乌斯三角形(英语:Möbius triangle)并且对应于一个没有重叠的镶嵌,其对称群称为一个三角群。在球面移共有3个莫比乌斯三角形加一个单参数族;在欧氏平面上有三个莫比乌斯三角形;而在罗氏双曲空间中有三个参数族的莫比乌斯三角形,并没有特例。
空间
[编辑]施瓦茨三角形所属的空间取决于其p、q、r值:
- 球面
- 欧氏平面
- 罗氏平面(双曲面)
图形表示
[编辑]施瓦茨三角形可以用三角图来表示。每个节点表示施瓦茨三角形的边(镜射)。每条边是由相应的反射阶数合理的数值标示,即π/顶点角。
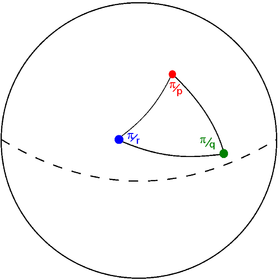 Schwarz triangle (p q r) on sphere |
 Schwarz triangle graph |
2阶边代表垂直于镜射,可以在该图中被忽略。在考克斯特 - 迪肯符号表示三角形图中会隐藏2阶边。 考克斯特组可用于更简单的符号,如(p q r)的循环图,(p q 2) = [p,q](直角三角形),和(p 2 2) = [p]×[]。
参考文献
[编辑]- ^ Schwarz, H. A., Ueber diejenigen Fälle in welchen die Gaussichen hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt, Journal für die reine und angewandte Mathematik, 1873, 75: 292–335 [2014-05-28], ISSN 0075-4102, (原始内容存档于2020-08-09) (Note that Coxeter references this as "Zur Theorie der hypergeometrischen Reihe", which is the short title used in the journal page headers)
- Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Table 3: Schwarz's Triangles)
- Wenninger, Magnus J., An introduction to the notion of polyhedral density, Spherical models, CUP Archive: 132–134, 1979, ISBN 978-0-521-22279-2
外部链接
[编辑]- 埃里克·韦斯坦因. Schwarz triangle. MathWorld.
- Klitzing, Richard. 3D The general Schwarz triangle (p q r) and the generalized incidence matrices of the corresponding polyhedra. bendwavy.org.



