隐失波

“Evanescent wave”的各地常用译名
中国大陆	隐失波、消散波、倏逝波、晕失波、消逝波、迅逝波
台湾	渐逝波、消散波、渐消波、衰减波、倏逝波、损耗波

沿金属-电介质界面传播的表面波（表面等离激元）的示意图。 远离表面的场以指数方式消失（右图），因此这些场在z方向上被描述为渐逝。

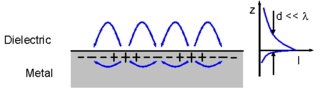
隐失波（英语：evanescent wave，又称为渐逝波、消逝波、消散波、倏逝波、衰逝波等）是指当光波从光密介质入射到光疏介质时，发生全反射而光疏介质一侧所产生的一种电磁波。由于其振幅随与分界面垂直的深度的增大而呈指数形式衰减，而随切线方向改变相位，因此也是一种表面波。隐失波是近场的，强度随着呈指数衰减的，没有被吸收的，其解是距边界的距离x的函数。隐失波作为波动方程的解，可以运用于任何波动方程。形成于两种拥有不同的波动性质的介质的边界上。在距离表面三分之一波长的距离下最为强烈。特别的，隐失波可以发生在除了光学的其它情况下，如电磁辐射、声学、机械波的情况下。

原理

当光由光密介质（折射率为 n₁）入射到光疏介质（折射率为n₂）时，入射角为θ_i则折射角由斯涅尔定律（Snell’s law）可得为θ_t，可由以下数学式表示：$n_{1}\sin \theta _{i}=n_{2}\sin \theta _{t}$。

接着改变入射角θ_i使其慢慢增大，直到折射角θ_t为90度，我们称此入射角为临界角θ_c，接着继续增加入射角 $\theta _{i}$ 使其大于临界角 $\theta _{c}$，此时光波产生全内反射。

在光密介质 $n_{1}$ 内，反射波与入射波干涉，在界面附近形成驻波，而极小部分的能量会渗入光疏介质 $n_{2}$ ，电磁场会透出一段距离并沿着界面传播此即为隐失波。

隐失波的强度是随着与界面传播的距离成指数衰减的关系，透出一小段距离 $\delta _{z}$ 称为穿透深度dp（depth of penetration），其定义为当穿透之光波强度减弱至原光波强度的三分之一(1/e=36.8%)时的距离。

$\delta _{z}={\frac {\frac {\lambda }{2\pi }}{\sqrt {\left({\frac {n_{1}}{n_{2}}}\right)^{2}\sin ^{2}\theta _{i}-1}}}$

采用受抑全内反射的方法可以探测该隐失波的衰减程度，因此其可用来测量两表面间的距离，进而得知上下两表面的共同粗糙度。

应用

隐失波在各个领域都有广泛的应用。在光学上特别广泛。 例如利用隐失波原理制成的分光镜如图。

分光镜示意图。

如果只有单片棱镜，光线发生全反射。而使用两片棱镜，改变棱镜间的空气间隙大小，则能改变分光的比例。同样的原理，也可以在光纤的外层上加一光密物质从而得到光纤内部的性质。

参见

• 电磁波
• 全内反射
• 斯涅尔定律