MD5
| 概述 | |
|---|---|
| 设计者 | 罗纳德·李维斯特 |
| 首次发布 | 1992年4月 |
| 系列 | MD2、MD4、MD5、MD6 |
| 密码细节 | |
| 摘要长度 | 128位 |
| 分组长度 | 512位 |
| 结构 | Merkle–Damgård construction |
| 重复回数 | 4[1] |
MD5消息摘要算法(英语:MD5 Message-Digest Algorithm),一种被广泛使用的密码散列函数,可以产生出一个128位(16个字节)的散列值(hash value),用于确保资讯传输完整一致。MD5由美国密码学家罗纳德·李维斯特(Ronald Linn Rivest)设计,于1992年公开,用以取代MD4算法。这套算法的程序在 RFC 1321 中被加以规范。
将数据(如一段文字)运算变为另一固定长度值,是散列算法的基础原理。
1996年后被证实存在弱点,可以被加以破解,对于需要高度安全性的资料,专家一般建议改用其他算法,如SHA-2。2004年,证实MD5算法无法防止碰撞攻击,因此不适用于安全性认证,如SSL公开密钥认证或是数码签名等用途。
历史与密码学
[编辑]1992年8月,罗纳德·李维斯特向互联网工程任务组(IETF)提交了一份重要文件,描述了这种算法的原理。由于这种算法的公开性和安全性,在90年代被广泛使用在各种程序语言中,用以确保资料传递无误等。[2]
MD5由MD4、MD3、MD2改进而来,主要增强算法复杂度和不可逆性。
应用
[编辑]MD5曾被用于文件校验、SSL/TLS、IPsec、SSH,但MD5早已被发现有明显的缺陷。
算法
[编辑]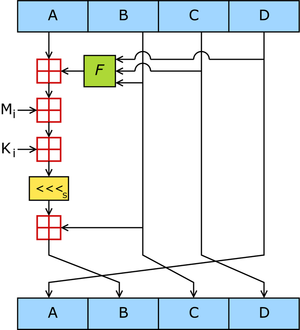
MD5是输入不定长度资讯,输出固定长度128-bits的算法。经过程序流程,生成四个32位数据,最后联合起来成为一个128-bits散列。基本方式为,求余、取余、调整长度、与链接变量进行循环运算。得出结果。
是 XOR, AND, OR , NOT 的符号。
伪代码
[编辑]//Note: All variables are unsigned 32 bits and wrap modulo 2^32 when calculating
var int[64] r, k
//r specifies the per-round shift amounts
r[ 0..15]:= {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22}
r[16..31]:= {5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20}
r[32..47]:= {4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23}
r[48..63]:= {6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21}
//Use binary integer part of the sines of integers as constants:
for i from 0 to 63
k[i] := floor(abs(sin(i + 1)) × 2^32)
//Initialize variables:
var int h0 := 0x67452301
var int h1 := 0xEFCDAB89
var int h2 := 0x98BADCFE
var int h3 := 0x10325476
//Pre-processing:
append "1" bit to message
append "0" bits until message length in bits ≡ 448 (mod 512)
append bit length of message as 64-bit little-endian integer to message
//Process the message in successive 512-bit chunks:
for each 512-bit chunk of message
break chunk into sixteen 32-bit little-endian words w[i], 0 ≤ i ≤ 15
//Initialize hash value for this chunk:
var int a := h0
var int b := h1
var int c := h2
var int d := h3
//Main loop:
for i from 0 to 63
if 0 ≤ i ≤ 15 then
f := (b and c) or ((not b) and d)
g := i
else if 16 ≤ i ≤ 31
f := (d and b) or ((not d) and c)
g := (5×i + 1) mod 16
else if 32 ≤ i ≤ 47
f := b xor c xor d
g := (3×i + 5) mod 16
else if 48 ≤ i ≤ 63
f := c xor (b or (not d))
g := (7×i) mod 16
temp := d
d := c
c := b
b := leftrotate((a + f + k[i] + w[g]),r[i]) + b
a := temp
Next i
//Add this chunk's hash to result so far:
h0 := h0 + a
h1 := h1 + b
h2 := h2 + c
h3 := h3 + d
End ForEach
var int digest := h0 append h1 append h2 append h3 //(expressed as little-endian)
MD5散列
[编辑]一般128位的MD5散列被表示为32位十六进制数字。以下是一个43位长的仅ASCII字母列的MD5散列:
MD5("The quick brown fox jumps over the lazy dog")
= 9e107d9d372bb6826bd81d3542a419d6
即使在原文中作一个小变化(比如用c取代d)其散列也会发生巨大的变化:
MD5("The quick brown fox jumps over the lazy cog")
= 1055d3e698d289f2af8663725127bd4b
空文的散列为:
MD5("")
= d41d8cd98f00b204e9800998ecf8427e
缺陷
[编辑]2004年的国际密码讨论年会(CRYPTO)尾声,王小云及其研究同事展示了寻找MD5、SHA-0及其他相关散列函数的散列冲撞的新方法[3]。所谓散列冲撞指两个完全不同的消息经散列函数计算得出完全相同的散列值。根据鸽巢原理,以有长度限制的散列函数计算没有长度限制的消息是必然会有冲撞情况出现的。在此之前,已有一些研究者在有约束条件下找到多对哈希冲撞[4][5]。
2009年,中国科学院的谢涛和冯登国仅用了220.96的碰撞算法复杂度,破解了MD5的碰撞抵抗,该攻击在普通电脑上运行只需要数秒钟[6]。2011年,RFC 6151 禁止MD5用作密钥散列消息认证码。
参见
[编辑]参考文献
[编辑]- ^ RFC 1321, section 3.4, "Step 4. Process Message in 16-Word Blocks", page 5.
- ^ 梁斌. 第3章“搜索引擎的下载系统”第4节“网页抓取原理”. 走进搜索引擎. 孙学瑛 (责任编辑) 第1版. 电子工业出版社. 2007年10月: 51. ISBN 978-7-121-04922-4 (中文(中国大陆)).
- ^ Wang, Xiaoyun; Feng, Dengguo; Lai, Xuejia; Yu, Hongbo. Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD. 2020-06-09 [2020-06-09]. (原始内容存档于2020-06-09) –通过ePrint IACR.
- ^ den Boer, Bert; Bosselaers, Antoon. Collisions for the compression function of MD5. Advances in Cryptology — EUROCRYPT ’93. Berlin, Heidelberg: Springer Berlin Heidelberg. 1994: 293–304. ISBN 978-3-540-57600-6. ISSN 0302-9743. doi:10.1007/3-540-48285-7_26.
- ^ Wang, Xiaoyun; Lai, Xuejia; Feng, Dengguo; Chen, Hui; Yu, Xiuyuan. Cryptanalysis of the Hash Functions MD4 and RIPEMD. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg. 2005: 1–18. ISBN 978-3-540-25910-7. ISSN 0302-9743. doi:10.1007/11426639_1.
- ^ Tao Xie and Dengguo Feng. How To Find Weak Input Differences For MD5 Collision Attacks (PDF). 30 May 2009 [2010-09-21]. (原始内容存档 (PDF)于2012-05-05).
- Berson, Thomas A. Differential Cryptanalysis Mod 232 with Applications to MD5. EUROCRYPT: 71–80. 1992. ISBN 978-3-540-56413-3.
- Bert den Boer; Antoon Bosselaers. Collisions for the Compression Function of MD5. 1993: 293–304. ISBN 978-3-540-57600-6.
|booktitle=被忽略 (帮助) - Hans Dobbertin, Cryptanalysis of MD5 compress. Announcement on Internet, May 1996 [1] (页面存档备份,存于互联网档案馆).
- Dobbertin, Hans. The Status of MD5 After a Recent Attack. CryptoBytes. 1996, 2 (2) [2006-07-30]. (原始内容存档于2006-08-13).
- Cong, Zijie. 提高哈希安全性的一些错误做法. Clifton Labratory. 2009.[失效链接]





