分子動力學


分子動力學是一套分子模擬方法,該方法主要是依靠計算機來模擬分子、原子體系的運動,是一種多體模擬方法。通過對分子、原子在一定時間內運動狀態的模擬,從而以動態觀點考察系統隨時間演化的行為。通常,分子、原子的軌跡是通過數值求解牛頓運動方程式得到,位能(或其對笛卡爾坐標的一階偏導數,即力)通常可以由分子間交互作用位能函數、分子力學力場、全始計算給出。對於考慮分子本身的量子效應的體系,往往採用波包近似處理或採用量子力學的費恩曼路徑積分表述方式[1]處理。 分子動力學也常常被採用作為研究複雜體系熱力學性質的採樣方法。在分子體系的不同狀態構成的系綜中抽取樣本,從而計算體系的構型積分,並以構型積分的結果為基礎進一步計算體系的熱力學量和其他宏觀性質。 分子動力學最早在20世紀50年代由物理學家提出,如今廣泛應用於物理、化學、生物體系的理論研究中。
分子動力學簡史[編輯]
- 1957年:基於剛球勢的分子動力學法(Alder and Wainwright)
- 1964年:利用Lennard-Jones勢函數法對液態氬性質的模擬(Rahman)
- 1971年:模擬具有分子團簇行為的水的性質(Rahman and Stillinger)
- 1977年:約束動力學方法(Rychaert, Ciccotti & Berendsen; van Gunsteren)
- 1980年:恆壓條件下的動力學方法(Andersen法、Parrinello-Rahman法)
- 1983年:非平衡態動力學方法(Gillan and Dixon)
- 1984年:恆溫條件下的動力學方法(Berendsen et al.)
- 1984年:恆溫條件下的動力學方法(Nosé-Hoover法)
- 1985年:第一原理分子動力學法(→Car-Parrinello法)
- 1991年:巨正則系綜的分子動力學方法(Cagin and Pettit)
- 1993年:路徑積分分子動力學
基本步驟[編輯]
- 確定起始構型
- 進行分子動力學模擬的第一步是確定起始構型, 一個能量較低的起始構型是進行分子模擬的基礎 ,一般分子的起始構型主要來自實驗數據或量子化學計算。
- 在確定起始構型之後要賦予構成分子的各個原子速度,這一速度是根據波茲曼分布隨機生成的,由於速度的分布符合波茲曼統計,因此在這個階段,體系的溫度是恆定的。另外,在隨機生成各個原子的運動速度之後須進行調整,使得體系總體在各個方向上的動量之和為零,即保證體系沒有平動位移。
- 進入平衡相
- 由上一步確定的分子組建平衡相,在構建平衡相的時候會對構型、溫度等參數加以監控。
- 進入生產相
- 進入生產相之後體系中的分子和分子中的原子開始根據初始速度運動,可以想像其間會發生吸引、排斥乃至碰撞,這時就根據牛頓力學和預先給定的粒子間交互作用勢來對各個粒子的運動軌跡進行計算,在這個過程中,體系總能量不變,但分子內部位能和動能不斷相互轉化,從而體系的溫度也不斷變化,在整個過程中,體系會遍歷位能面上的各個點(理論上,如果模擬時間無限)。計算分析所用樣本正是從這個過程中抽取的。
- 計算結果
- 用抽樣所得體系的各個狀態計算當時體系的位能,進而計算構型積分。
作用勢與動力學計算[編輯]
作用勢的選擇與動力學計算的關係極為密切,選擇不同的作用勢,體系的位能面會有不同的形狀,動力學計算所得的分子運動 和 分子內部運動的軌跡也會不同,進而影響到抽樣的結果和抽樣結果的位能計算,最初的分子動力學計算採用比較簡單的剛球勢,現在更多地採用蘭納-瓊斯勢,後者能夠更好的與粒子間交互作用擬合。
時間步長與約束動力學[編輯]
分子動力學計算的基本思想是賦予分子體系初始運動狀態之後利用分子的自然運動在相空間中抽取樣本進行統計計算,時間步長就是抽樣的間隔,因而時間步長的選取對動力學模擬非常重要。太長的時間步長會造成分子間的激烈碰撞,體系數據溢出;太短的時間步長會降低模擬過程搜索相空間的能力,因此一般選取的時間步長為體系各個自由度中最短運動週期的十分之一。
但是通常情況下,體系各自由度中運動週期最短的是各個化學鍵的振動,而這種運動對計算某些 宏觀性質 並不產生影響,因此就產生了屏蔽分子內部振動或其他無關運動的約束動力學,約束動力學可以有效地增長分子動力學模擬的時間步長,提高搜索相空間的能力。
應用[編輯]
分子動力學的計算過程給定了體系的總能量,因此適用於對微正則系綜的模擬計算,另外由於分子動力學計算過程始終是時間的函數,因此一些與時間有關的巨觀量如擴散係數的模擬必須應用分子動力學。
另外,在實際應用中,經常把分子動力學方法和蒙特·卡羅方法聯合使用。 在近年,多尺度模擬計算已經得到了很多學者的關注。在多尺度模擬計算中,分子動力學方法研究奈米級現象,蒙特·卡羅方法研究微觀形態,有限元方法應用於宏觀領域。通過多種尺度的多種模擬計算方法的聯合應用,令納觀與宏觀聯結起來。
應用的領域和限制[編輯]
設計約束[編輯]
微正則系綜(NVE)[編輯]
正則系綜(NVT)[編輯]
等溫等壓系綜(NPT)[編輯]
通用化系綜[編輯]
MD模擬中的勢函數[編輯]
經驗勢函數[編輯]
Pair勢與多體勢函數[編輯]
半經驗勢函數[編輯]
極化勢函數[編輯]
第一性原理方法中的勢函數[編輯]
混合QM/MM[編輯]
粗粒化和約化表示[編輯]
長程作用力[編輯]
受控分子動力學(Steered MD)[編輯]
應用案例[編輯]
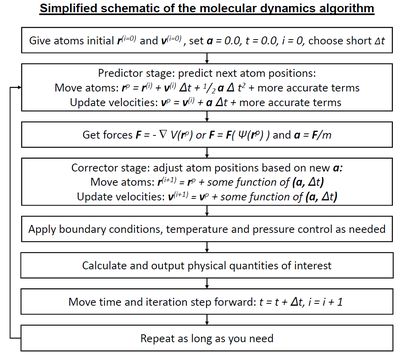
分子動力學算法[編輯]
積分器[編輯]
短程作用算法[編輯]
長程作用算法[編輯]
並行策略[編輯]
從頭算分子動力學[編輯]
MD模擬的專用硬體[編輯]
圖形卡上的MD模擬[編輯]
參見[編輯]
參考資料[編輯]
- ^ Efficient molecular dynamics and hybrid Monte Carlo algorithms for path integrals, Tuckerman et al, The Journal of Chemical Physics, 99, 2796(1993) http://dx.doi.org/10.1063/1.465188
外部連結[編輯]
- (英文)The GPUGRID.net Project (頁面存檔備份,存於網際網路檔案館) (GPUGRID.net)
- (英文)The Blue Gene Project (IBM)JawBreakers.org
- (英文)Materials modelling and computer simulation codes (頁面存檔備份,存於網際網路檔案館)
- (英文)A few tips on molecular dynamics (頁面存檔備份,存於網際網路檔案館)
- (英文)Movie of MD simulation of water (Youtube) (頁面存檔備份,存於網際網路檔案館)
- (英文)Live molecular dynamics simulation rendered at 1 frame per second (頁面存檔備份,存於網際網路檔案館)
- (英文)Molecular Dynamics Simulation; 7 Essential Concepts You Need to Learn (頁面存檔備份,存於網際網路檔案館) }


