在數學上,錐狀分布 (Cone-shaped distribution function)是科恩克萊斯分佈 系列函數中的一種。錐狀分布於西元1991年由 Yunxin Zhao、Les E. Atlas 和 Robert J. Marks 提出。本分布之核心函數
ϕ
(
t
,
τ
)
{\displaystyle \phi \left(t,\tau \right)}
t
,
τ
{\displaystyle t,\tau }
錐狀分布的定義如下
C
x
(
t
,
f
)
=
∫
−
∞
∞
∫
−
∞
∞
A
x
(
η
,
τ
)
Φ
(
η
,
τ
)
exp
(
j
2
π
(
η
t
−
τ
f
)
)
d
η
d
τ
{\displaystyle C_{x}(t,f)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }A_{x}(\eta ,\tau )\Phi (\eta ,\tau )\exp(j2\pi (\eta t-\tau f))\,d\eta \,d\tau }
其中
A
x
(
η
,
τ
)
=
∫
−
∞
∞
x
(
t
+
τ
/
2
)
x
∗
(
t
−
τ
/
2
)
e
−
j
2
π
t
η
d
t
{\displaystyle A_{x}(\eta ,\tau )=\int _{-\infty }^{\infty }x(t+\tau /2)x^{*}(t-\tau /2)e^{-j2\pi t\eta }\,dt}
其核心函數
Φ
(
η
,
τ
)
{\displaystyle \Phi \left(\eta ,\tau \right)}
Φ
(
η
,
τ
)
=
sin
(
π
η
τ
)
π
η
τ
exp
(
−
2
π
α
τ
2
)
{\displaystyle \Phi \left(\eta ,\tau \right)={\frac {\sin \left(\pi \eta \tau \right)}{\pi \eta \tau }}\exp \left(-2\pi \alpha \tau ^{2}\right)}
其中
α
{\displaystyle \alpha }
由
ϕ
(
t
,
τ
)
=
F
−
1
[
Φ
(
η
,
τ
)
]
{\displaystyle \phi \left(t,\tau \right)={\mathcal {F}}^{-1}\left[\Phi \left(\eta ,\tau \right)\right]}
ϕ
(
t
,
τ
)
=
{
1
τ
exp
(
−
2
π
α
τ
2
)
,
|
τ
|
≥
2
|
t
|
,
0
,
otherwise
.
{\displaystyle \phi \left(t,\tau \right)={\begin{cases}{\frac {1}{\tau }}\exp \left(-2\pi \alpha \tau ^{2}\right),&|\tau |\geq 2|t|,\\0,&{\mbox{otherwise}}.\end{cases}}}
下圖為錐狀分布之核心函數於
t
,
τ
{\displaystyle t,\tau }
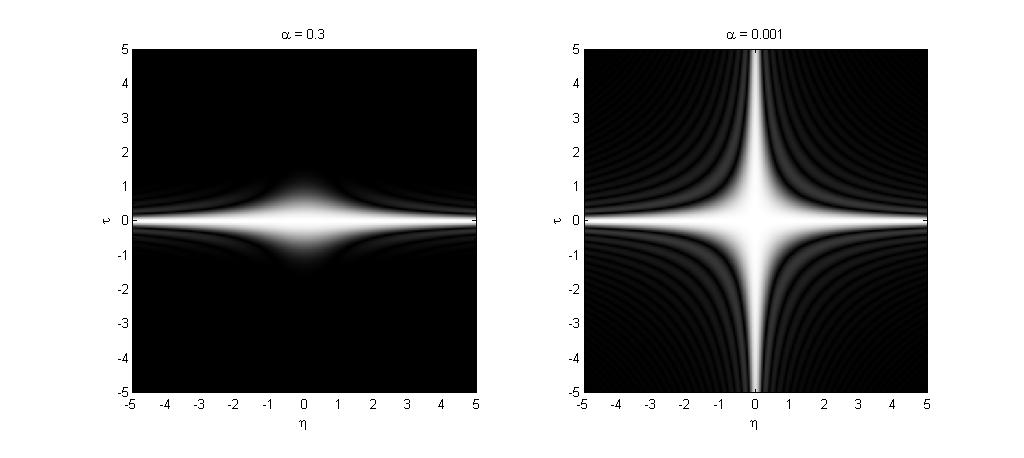
下列圖形為錐狀分布之核心函數於
η
,
τ
{\displaystyle \eta ,\tau }
α
{\displaystyle \alpha }
觀察上圖可知,我們可以透過選取適當的
α
{\displaystyle \alpha }
Φ
(
η
,
τ
)
{\displaystyle \Phi \left(\eta ,\tau \right)}
τ
{\displaystyle \tau }
當輸入信號由二具有相同或相近中心頻率的成分組成,使用錐狀分布作為核心函數可以完全濾除交叉項。相反地,本分布無法濾除當輸入信號由二具有相同或相近中心時間的成分組成所形成之交叉項。
Time frequency analysis and wavelet transform class notes (頁面存檔備份 ,存於網際網路檔案館 ), Jian-Jiun Ding, the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2007.S. Qian and D. Chen, Joint Time-Frequency Analysis: Methods and Applications, Chap. 5, Prentice Hall, N.J., 1996.
H. Choi and W. J. Williams, 「Improved time-frequency representation of multicomponent signals using exponential kernels,」 IEEE. Trans. Acoustics, Speech, Signal Processing, vol. 37, no. 6, pp. 862–871, June 1989.
Y. Zhao, L. E. Atlas, and R. J. Marks, 「The use of cone-shape kernels for generalized time-frequency representations of nonstationary signals,」 IEEE Trans. Acoustics, Speech, Signal Processing, vol. 38, no. 7, pp. 1084–1091, July 1990. 







![{\displaystyle \phi \left(t,\tau \right)={\mathcal {F}}^{-1}\left[\Phi \left(\eta ,\tau \right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26bf00237868fd24da2be4f697c9bbfd81c1d5f5)