File:StationaryStatesAnimation.gif
外觀
StationaryStatesAnimation.gif (300 × 280 像素,檔案大小:223 KB,MIME 類型:image/gif、循環、41 畫格)
檔案歷史
點選日期/時間以檢視該時間的檔案版本。
| 日期/時間 | 縮圖 | 尺寸 | 使用者 | 備註 | |
|---|---|---|---|---|---|
| 目前 | 2011年3月20日 (日) 18:21 | 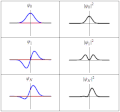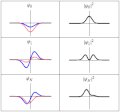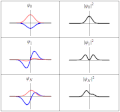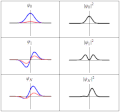 | 300 × 280(223 KB) | Sbyrnes321 | {{Information |Description ={{en|1=Three wavefunction solutions to the Time-Dependent Schrödinger equation for a harmonic oscillator. Left: The real part (blue) and imaginary part (red) of the wavefunction. Right: The probability of finding the partic |
檔案用途
全域檔案使用狀況
以下其他 wiki 使用了這個檔案:
- ar.wikipedia.org 的使用狀況
- ast.wikipedia.org 的使用狀況
- az.wikipedia.org 的使用狀況
- bn.wikipedia.org 的使用狀況
- bs.wikipedia.org 的使用狀況
- de.wikipedia.org 的使用狀況
- el.wikipedia.org 的使用狀況
- en.wikipedia.org 的使用狀況
- eo.wikipedia.org 的使用狀況
- es.wikipedia.org 的使用狀況
- fa.wikipedia.org 的使用狀況
- ga.wikipedia.org 的使用狀況
- gl.wikipedia.org 的使用狀況
- he.wikipedia.org 的使用狀況
- hy.wikipedia.org 的使用狀況
- ia.wikipedia.org 的使用狀況
- id.wikipedia.org 的使用狀況
- ja.wikipedia.org 的使用狀況
- lt.wikipedia.org 的使用狀況
- mk.wikipedia.org 的使用狀況
- pa.wikipedia.org 的使用狀況
- pl.wikipedia.org 的使用狀況
- pnb.wikipedia.org 的使用狀況
- ro.wikipedia.org 的使用狀況
- sl.wikipedia.org 的使用狀況
- ta.wikipedia.org 的使用狀況
- tl.wikipedia.org 的使用狀況
- tr.wikipedia.org 的使用狀況
- uk.wikipedia.org 的使用狀況
- uz.wikipedia.org 的使用狀況
- vi.wikipedia.org 的使用狀況
- www.wikidata.org 的使用狀況



