三段論
外觀
(重新導向自大前提)

三段論在傳統邏輯中,是在其中一個命題(結論)必然地從另外兩個命題(叫做前提)中得出的一種推論。這個定義是傳統的,可以寬鬆地從亞里斯多德的《前分析篇》Book I, c. 1中推出來。希臘語「sullogismos」的意思是「演繹」。對傳統意義上的三段論的詳細描述參見直言三段論。[1]
三段論由三個部分組成:大前提、小前提和結論。邏輯上,結論是於小前提之上應用大前提得到的。大前提是一般性的原則,小前提是一個特殊陳述。
正式定義
[編輯]在數理邏輯裡,三段論證可以能代表:(若 、 、 都為合式公式)
但另一方面,若
成立,則也會被稱為以 和 為前提, 為結論的三段論證。
範例
[編輯]嚴謹地說,這段論證宣稱
這個論證會正確,是基於
和
- 若 ,那就會有
另一方面,含常數符號(特殊個體)的例子如
- 所有人(M)都是必死的(D),(大前提):
- 蘇格拉底(S)是人(M),(小前提):
- 蘇格拉底是必死的。(結論):
上面的例子也可以抽換成
有效性
[編輯]與之相對的是隱喻,它組織叫做肯定後件的一種形式的三段論,是邏輯謬論:
Barbara三段論涉及文法和邏輯類型;它有一個主詞(比如蘇格拉底)和一個謂詞(必死的)。肯定後件,是隱喻的基礎。這種形式的三段論是邏輯上無效的。
歸納論證(epagoge)是依賴於歸納推理的弱三段論。
24論式圖示
[編輯]下表以文氏圖展示24個有效直言三段論,不同欄表示不同的前提,不同外框顏色表示不同的結論,需要存在性預設的推理以虛線與斜體字標示。
| 格 | A ∧ A | A ∧ E | A ∧ I | A ∧ O | E ∧ I | ||||||
| AAA | AAI | AEE | AEO | EAE | EAO | AII | IAI | AOO | OAO | EIO | |
| 1 | 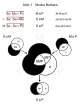 Barbara |
 Barbari |
 Celarent |
 Celaront |
 Darii |
 Ferio | |||||
| 2 |  Camestres |
 Camestros |
 Cesare |
 Cesaro |
 Baroco |
 Festino | |||||
| 3 |  Darapti |
 Felapton |
 Datisi |
 Disamis |
 Bocardo |
 Ferison | |||||
| 4 |  Bamalip |
 Calemes |
 Calemos |
 Fesapo |
 Dimatis |
 Fresison |
參見
[編輯]參考文獻
[編輯]- ^ 朱建平. 亚里士多德逻辑的现代性研究. 中國社會科學網. 中國大陸: 中國社會科學院. 2019-11-07 [2020-10-05]. (原始內容存檔於2022-02-26) (中文(簡體)).
- ^ 01哲學團隊. 亞里士多德:邏輯作為方法 - EP12. 香港: 香港01. 2017-02-14 [2020-10-05]. (原始內容存檔於2022-02-26) (中文(繁體)).
外部連結
[編輯]- Abbreviatio Montana(頁面存檔備份,存於網際網路檔案館) article by Prof. R. J. Kilcullen of Macquarie University on the medieval classification of syllogisms.
- The Figures of the Syllogism(頁面存檔備份,存於網際網路檔案館) is a brief table listing the forms of the syllogism.
- Stanford Encyclopedia of Philosophy entry on Medieval Theories of Syllogisms(頁面存檔備份,存於網際網路檔案館)
| 傳統邏輯:三段論 |
| 形式:直言三段論 | 選言三段論 | 假言三段論 | 複合三段論 | 準三段論 | 統計三段論 |
| 其他:對立四邊形 | 布林三段論 | 三段論謬論 |






![{\displaystyle \forall x[M(x)\Rightarrow D(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/840ba037a27ddc4edaa834462bc02dfe659db1cc)
![{\displaystyle \forall x[G(x)\Rightarrow M(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a56be07ee3f9b75ca1ef369ae9c6c52b9f5637)
![{\displaystyle \forall x[G(x)\Rightarrow D(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aca1073517ee380ceb3a1c0847da0cc63d6810f)
![{\displaystyle \forall x[M(x)\Rightarrow D(x)],\,\forall x[G(x)\Rightarrow M(x)]\vdash \forall x[G(x)\Rightarrow D(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4294c85d536e9735a63b809333a7d427d19f4415)






