蜘蛛圖
蜘蛛圖比歐拉圖多增加了存在點。這種點代表了歐拉圖中的交集或是邏輯與(AND)條件,這些點的連接則代表了邏輯或(OR)條件。這些線連在一起形成像蜘蛛一樣的形狀,也就是這種圖被命名為蜘蛛圖的原因。
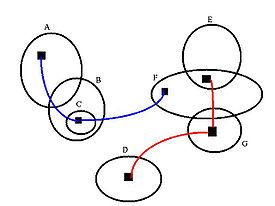
舉例來說,在右圖存在以下交集
除了上述指定的交集之外, A、B 和 D 到G 這些集合是可分開獲得的,集合 C 只能是 B 的子集。在複雜的圖中,單元素集合與/或合取經常有可能被其他集合組合所遮掩。
在這個例子中的兩個蜘蛛分別對應於下列邏輯表達式:
紅蜘蛛:
藍蜘蛛:
進階讀物[編輯]
- Stapleton, G. and Howse, J. and Taylor, J. and Thompson, S. What can spider diagrams say Proc. Diagrams, (2004) v. 168, pgs 169-219 Accessed on July 31, 2012 here






