有固定焦点 (几何) F 和準線的橢圓形 (e = 1/2) ,拋物線(e = 1) 和 雙曲線(e = 2) 。 二次曲面 (英語:Quadrics )指任何n 維的超曲面 ,其定義為多元二次方程 的解的軌跡。
在坐标
{
x
0
,
x
1
,
x
2
,
…
,
x
D
}
{\displaystyle \{x_{0},x_{1},x_{2},\ldots ,x_{D}\}}
[1]
∑
i
,
j
=
0
D
Q
i
,
j
x
i
x
j
+
∑
i
=
0
D
P
i
x
i
+
R
=
0
{\displaystyle \sum _{i,j=0}^{D}Q_{i,j}x_{i}x_{j}+\sum _{i=0}^{D}P_{i}x_{i}+R=0}
上式亦可以用矩陣乘法 和向量 的內積 等概念,寫成以下形式:
x
=
(
x
1
x
2
⋮
x
n
)
;
{\displaystyle \mathbf {x} ={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\\\end{pmatrix}};}
A
=
(
a
11
a
12
⋯
a
1
n
a
12
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
1
n
a
2
n
⋯
a
n
n
)
;
{\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{12}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{1n}&a_{2n}&\cdots &a_{nn}\\\end{pmatrix}};}
b
=
(
b
1
b
2
⋮
b
n
)
{\displaystyle \mathbf {b} ={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{n}\end{pmatrix}}}
⟨
A
x
,
x
⟩
+
⟨
b
,
x
⟩
+
c
=
0
{\displaystyle \langle A\mathbf {x} ,\mathbf {x} \rangle +\langle \mathbf {b} ,\mathbf {x} \rangle +c=0}
二次曲面是代數簇 的一種。
欧几里得空间 [ 编辑 ] 二次曲面的方程为:
Q
=
{
(
x
,
y
,
z
)
∈
R
3
∣
A
x
2
+
B
y
2
+
C
z
2
+
D
x
y
+
E
y
z
+
F
x
z
+
G
x
+
H
y
+
I
z
+
J
=
0
}
{\displaystyle Q=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0\right\}}
未退化 的一般实二次曲面
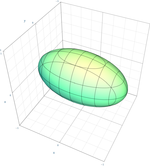
橢球 面
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}
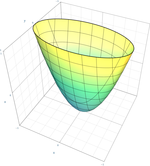
橢圓拋物面
x
2
a
2
+
y
2
b
2
−
z
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,}
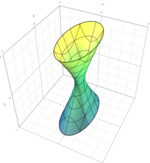
雙曲拋物面
x
2
a
2
−
y
2
b
2
−
z
=
0
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,}
單葉雙曲面
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}
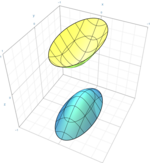
雙葉雙曲面
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
−
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}
退化的二次曲面
椭圆锥面
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}
橢圓柱面
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}
雙曲柱面
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}
拋物柱面
x
2
+
2
a
y
=
0
{\displaystyle x^{2}+2ay=0\,}
参考来源 [ 编辑 ]
^ [1] (页面存档备份 ,存于互联网档案馆 ), Quadrics in Geometry Formulas and Facts by Silvio Levy, excerpted from 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press).
外部链接 [ 编辑 ]