度分布

度分布是图论和网络理论中的概念。一个图(或网络)由一些顶点(节点)和连接它们的边(连结)构成。每个顶点(节点)连出的所有边(连结)的数量就是这个顶点(节点)的度。度分布指的是对一个图(网络)中顶点(节点)度数的总体描述。对于随机图,度分布指的是图中顶点度数的概率分布。
定义
[编辑]度分布是图论和(复杂)网络理论中都存在的概念。首先介绍图的概念。一个图是一个由两个集合和构成的二元组。集合一般由有限个元素构成:,其中的元素被称为图的顶点。集合是由个元素构成的集合:。中的每个元素都是一个非负整数。无向图中,的一个元素,表示中的两个顶点和连有条边,并且规定。有向图中,的一个元素,表示中的顶点有条连向顶点的边。如果一个图中所有的都不超过1,并且,那么称图是简单图。
网络理论的数学框架建立在图论上。网络理论中的网络其实就是图论中的图,但在网络理论中称之为网络,图的顶点在网络理论中称为节点,边被称为连结。以下仍旧以图论中的术语定义度分布。
一个无向图中某个顶点的度,是指所有与它相连的边的数目。
有向图中,根据连出边的数目和连入边的数目,分为出度和入度。
因此,一个无向图中,可以看成将每个顶点映射到一个非负整数的函数:
而度分布则是对每个非负整数,考察度数是的顶点在所有顶点中占的比例:
因此满足:
从顶点中等概率地随机抽取一个顶点,那么这个顶点度数为的概率就是。
随机图顶点的度分布
[编辑]随机图是指由随机过程产生的图,即是将给定的顶点之间随机地连上边。一个随机图中,每两个顶点之间的边的数量是随机变量。因此任一顶点的度也是随机变量。这个变量的概率分布也称为随机图中的顶点的度分布:
这个定义与一般的图的度分布是不一样的[2]。
在经典的随机图模型中,所有顶点的位置都是一致的,没有特殊的顶点。因此每个顶点的度分布都是相同的:。所以,随机抽取一个顶点,它的度数是的概率就是;越高,表示可能有更多的顶点度数是。当顶点数目很大每个顶点的度分布都是相对独立的时候,顶点的度分布近似等于图中度数是的顶点的比例[1]。
例子
[编辑]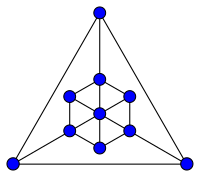
以下给出一些度分布的例子。右图是由十个顶点构成的无向图。其中度数是4的顶点有3个,度数是3的顶点有6个,度数是6的顶点有1个,所以度分布是:
对于阶完全图,所有的顶点的度数都是,所以度分布是:

如果图是任意两顶点之间以概率连边的随机图,那么每个顶点都有相同的度分布。
这个分布是泊松分布。我们可以构造每个顶点的度数都是这样的概率分布的随机图模型。这样当顶点数很大的时候,度数是的顶点的个数占的比例大致是。这个分布的特点是当k很小或很大的时候,都近似于0,的值在一个特定的值处达到高峰,然后回落。也就是说,大多数的顶点的度数在这个特定值左右。然而在真实的复杂网络中,人们观察到,度分布并不像这种随机图模型显示的,聚集在某个特定值周围,而是随着k增大而以多项式速度递减,也就是遵从所谓的幂律分布:
也就是说 的概率反比于 的某个幂次,其中是某个正实数。这种网络特性被称为无尺度特性[3][4]。
参考文献
[编辑]- 引用
- ^ 1.0 1.1 Newman, M. E. J. The structure and function of complex networks. SIAM Review. 2003, 45 (2): 167–256. Bibcode:2003SIAMR..45..167N. arXiv:cond-mat/0303516
 . doi:10.1137/S003614450342480.[永久失效連結]
. doi:10.1137/S003614450342480.[永久失效連結]
- ^ 2.0 2.1 M. E. J. Newman, S. H. Strogatz, D. J. Watts. Random Graphs with Arbitrary Degree Distribution and Their Applications. Phys. Rev. E. 2001, 64. doi:10.1103/PhysRevE.64.026118.
- ^ 《科学美国人》中文版2003年7月. 无尺度网络. 集智集团. [2011-07-04]. (原始内容存档于2012-01-11).
- ^ Albert-László Barabási, Réka Albert. Emergence of Scaling in Random Networks (PDF). Science: 509–512. [2013-04-19]. doi:10.1126/science.286.5439.509. (原始内容 (PDF)存档于2021-09-23).
- 期刊文章
- Albert, R.; Barabasi, A.-L. Statistical mechanics of complex networks. Reviews of Modern Physics. 2002, 74: 47–97. Bibcode:2002RvMP...74...47A. arXiv:cond-mat/0106096
 . doi:10.1103/RevModPhys.74.47.
. doi:10.1103/RevModPhys.74.47. - Dorogovtsev, S.; Mendes, J. F. F. Evolution of networks. Advances in Physics. 2002, 51 (4): 1079–1187. Bibcode:2002AdPhy..51.1079D. arXiv:cond-mat/0106144
 . doi:10.1080/00018730110112519.
. doi:10.1080/00018730110112519.
- 书籍
- Shlomo Havlin, Reuven Cohen. Complex Networks: Structure, Robustness and Function. Cambridge University Press. 2010 [2013-04-20]. (原始内容存档于2011-10-04).







































