随机变量是一種数学概念,用来表示随机试验结果的变量。
随机变量通常用大写字母 、
、 表示。在各种随机试验中,每一个随机事件都可以用一个变量代替任何一个数值。例如擲骰子時擲出的点数是1,2,..,6中的一个,其中的任意一个点数都可以用变量
表示。在各种随机试验中,每一个随机事件都可以用一个变量代替任何一个数值。例如擲骰子時擲出的点数是1,2,..,6中的一个,其中的任意一个点数都可以用变量 来表示,
来表示, 可以=1,=2....=6,又例如在产品的抽查中,抽到正品可以用“
可以=1,=2....=6,又例如在产品的抽查中,抽到正品可以用“ =1”来表示,抽到次品可以用“
=1”来表示,抽到次品可以用“ =0”来表示,这样
=0”来表示,这样 又可以=1也可以=0。[1],随机变量实质上是函数。称其为变量是指可作为因变量。
又可以=1也可以=0。[1],随机变量实质上是函数。称其为变量是指可作为因变量。
正式定義[编辑]
直觀上,随机变量為一種特殊的實函數,其值不大於某數的狀況都是事件。所以一個函數是不是隨機變量也跟「怎樣的子集合算事件」有密不可分的關係。
如果随机变量  的取值是有限的或者是可数无穷尽的值:
的取值是有限的或者是可数无穷尽的值:

则称  为离散随机变量。如果
为离散随机变量。如果  的取值遍布一区间甚至是整個數線:(
的取值遍布一区间甚至是整個數線:( )
)
![{\displaystyle X(S)=[a,\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df17530074a67b7e46f3c915cff7829ece9717b2)
则称 为连续随机变量。
为连续随机变量。
與可測函數的關係[编辑]
如果取  為所有實開區間所構成的集合:
為所有實開區間所構成的集合:
![{\displaystyle {\mathcal {I}}={\bigg \{}A\in {\mathcal {P}}(\mathbb {R} )\,{\bigg |}\,(\exists a)(\exists b)\left[\,(a,\,b\in \mathbb {R} )\wedge (A=(a,\,b))\,\right]{\bigg \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d0bd0ac0429611111bd22048ae71d327e7e57cb)
则可以把博雷爾代數  定義為包含
定義為包含  的最小Σ-代数:
的最小Σ-代数:

則根據阿基米德性質,對任意實數  ,
,![{\displaystyle (-\infty ,\,r]\in {\mathcal {B}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9e2cefbdce60da2e8821bca1926e11247a0a8b) ,有以下的關係:
,有以下的關係:
![{\displaystyle (r,\,\infty )=\bigcup \left\{A\in {\mathcal {I}}\,{\bigg |}\,(\exists n\in \mathbb {N} )\left[A=(r,\,n)\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c02dadb05b9092a3ca3b9807618361f38872b6a)
![{\displaystyle (-\infty ,\,r]=\mathbb {R} -(r,\,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bc762ee629f43a023a45a8cd254d44b3e91768)
反之,也可以用類似的方法,由任意的 ![{\displaystyle (-\infty ,\,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/960a6fafe2d4ddb72b638f794620827e8d069d6c) ,透過并集和补集組合出
,透過并集和补集組合出  :
:
![{\displaystyle (-\infty ,\,b)=\bigcup \left\{A\in {\mathcal {P}}(\mathbb {R} )\,{\bigg |}\,(\exists n\in \mathbb {N} )\left[A=(-\infty ,\,b-{\frac {1}{n}}]\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b540d9f91cffaf32042c5bbd4b2012abb66485)
![{\displaystyle (a,\,b)=\left(\mathbb {R} -(-\infty ,\,a]\right)\cup (-\infty ,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65909ed0997d08904c413d8e0fbbd9827ceee25b)
這樣的話,任意的  都有
都有 ,等價於對任意的
,等價於對任意的  都有
都有  ,這樣根據可测函数性质的定理(2),上小節定義的
,這樣根據可测函数性质的定理(2),上小節定義的  ,就是一個
,就是一個  -
-  可测函数,換句話說,随机变量是可測函數的一種特例。
可测函数,換句話說,随机变量是可測函數的一種特例。
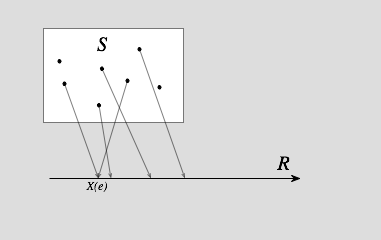 实数坐标轴上的随机变量示意图
实数坐标轴上的随机变量示意图
随机掷两个骰子,整个样本空间由36个元素组成:

然後可以簡單地把  的任意子集合都視為事件,換句話說,把事件族
的任意子集合都視為事件,換句話說,把事件族  取成
取成  的冪集:
的冪集:

這樣的話,可以構造出許多定義在  上的随机变量,比如
上的随机变量,比如  可以定義為「两个骰子的点数和」;者
可以定義為「两个骰子的点数和」;者  可以定義為「两个骰子的点数差」:
可以定義為「两个骰子的点数差」:


因為「两个骰子的点数和不大於  」和「两个骰子的点数差不大於
」和「两个骰子的点数差不大於  」的樣本點所構成的集合,都是
」的樣本點所構成的集合,都是  的子集合,所以
的子集合,所以  和
和  都是(在
都是(在  的意義下)定義在
的意義下)定義在  上的随机变量,而且它們都是离散随机变量。
上的随机变量,而且它們都是离散随机变量。
不确定性[编辑]
随机变量在不同的条件下由于偶然因素影响,其可能取各种随机变量不同的值,具有不确定性和随机性,但这些取值落在某个范围的概率是一定的,此种变量称为随机变量。随机变量可以是离散型的,也可以是连续型的。如分析测试中的测定值就是一个以概率取值的随机变量,被测定量的取值可能在某一范围内随机变化,具体取什么值在测定之前是无法确定的,但测定的结果是确定的,多次重复测定所得到的测定值具有统计规律性。随机变量与模糊变量的不确定性的本质差别在于,后者的测定结果仍具有不确定性,即模糊性。
基本类型[编辑]
简单地说,随机变量是指随机事件的数量表现。某地若干名男性健康成人中,每人血红蛋白量的测定值;等等。另有一些现象并不直接表现为数量,例如人口的男女性别、试验结果的阳性或阴性等,但我们可以规定男性为1,女性为0,则非数量标志也可以用数量来表示。这些例子中所提到的量,尽管它们的具体内容是各式各样的,但从数学观点来看,它们表现了同一种情况,这就是每个变量都可以随机地取得不同的数值,而在进行试验或测量之前,我们要预言这个变量将取得某个确定的数值是不可能的。
按照随机变量可能取得的值,可以把它们分为两种基本类型:
离散型随机变量[编辑]
即在一定区间内变量取值为有限个,或数值可以一一列举出来。例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等
连续型随机变量[编辑]
即在一定区间内变量取值有无限个,或数值无法一一列举出来。例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。
详细分析[编辑]
表示方法[编辑]
随机试验结果的量的表示。例如掷一颗骰子出现的点数,电话交换台在一定时间内收到的呼叫次数,随机抽查的一个人的身高,悬浮在液体中的微粒沿某一方向的位移,等等,都是随机变量的实例。
一个随机试验的可能结果(称为基本事件)的全体组成一个基本空间 (见概率)。随机变量
(见概率)。随机变量 是定义于
是定义于 上的函数,即对每一基本事件
上的函数,即对每一基本事件 ,有一数值
,有一数值 与之对应。以掷一颗骰子的随机试验为例,它的所有可能结果,共6个,分别记作
与之对应。以掷一颗骰子的随机试验为例,它的所有可能结果,共6个,分别记作 ,
,  ,
,  ,
,  ,
,  ,
,  ,这时,
,这时, ,而出现的点数这个随机变量
,而出现的点数这个随机变量 ,就是
,就是 上的函数
上的函数 ,
, 。又如设
。又如设 是要进行抽查的
是要进行抽查的 个人的全体,那么随意抽查其中一人的身高和体重,就构成两个随机变量
个人的全体,那么随意抽查其中一人的身高和体重,就构成两个随机变量 和
和 ,它们分别是
,它们分别是 上的函数:
上的函数: “
“ 的身高”,
的身高”, “
“ 的体重”,
的体重”, 。一般说来,一个随机变量所取的值可以是离散的(如掷一颗骰子的点数只取1到6的整数,电话台收到的呼叫次数只取非负整数),也可以充满一个数值区间,或整个实数轴(如液体中悬浮的微粒沿某一方向的位移)。
。一般说来,一个随机变量所取的值可以是离散的(如掷一颗骰子的点数只取1到6的整数,电话台收到的呼叫次数只取非负整数),也可以充满一个数值区间,或整个实数轴(如液体中悬浮的微粒沿某一方向的位移)。
研究方法[编辑]
在研究随机变量的性质时,确定和计算它取某个数值或落入某个数值区间内的概率是特别重要的。因此,随机变量取某个数值或落入某个数值区间这样的基本事件的集合,应当属于所考虑的事件域。根据这样的直观想法,利用概率论公理化的语言,取实数值的随机变量的数学定义可确切地表述如下:概率空间 上的随机变量
上的随机变量 是定义于
是定义于 上的实值可测函数,即对任意
上的实值可测函数,即对任意 ,
, 为实数,且对任意实数
为实数,且对任意实数 ,使
,使 的一切
的一切 组成的
组成的 的子集
的子集 是事件,也即是
是事件,也即是 中的元素。事件
中的元素。事件 常简记作
常简记作 ,并称函数
,并称函数 ,
, ,为
,为 的分布函数。
设
的分布函数。
设 ,
,  是概率空间
是概率空间 上的两个随机变量,如果除去一个零概率事件外,
上的两个随机变量,如果除去一个零概率事件外, 与
与 相同,则称
相同,则称 以概率1成立,也记作
以概率1成立,也记作 或
或 ,α.s.(α.s.意即几乎必然)。
,α.s.(α.s.意即几乎必然)。
有些随机现象需要同时用多个随机变量来描述。例如对地面目标射击,弹着点的位置需要两个坐标才能确定,因此研究它要同时考虑两个随机变量,一般称同一概率空间 上的
上的 个随机变量构成的
个随机变量构成的 维向量
维向量 为
为 维随机向量。随机变量可以看作一维随机向量。称
维随机向量。随机变量可以看作一维随机向量。称 元
元 的函数为
的函数为 的(联合)分布函数。又如果
的(联合)分布函数。又如果 为二维随机向量,则称
为二维随机向量,则称 为复随机变量。
随机变量的独立性 独立性是概率论所独有的一个重要概念。设
为复随机变量。
随机变量的独立性 独立性是概率论所独有的一个重要概念。设 是
是 个随机变量,如果对任何
个随机变量,如果对任何 个实数
个实数 都有 即它们的联合分布函数
都有 即它们的联合分布函数 等于它们各自的分布函数
等于它们各自的分布函数 的乘积。则称
的乘积。则称 是独立的。这一定义可以直接推广到每一
是独立的。这一定义可以直接推广到每一 (
( )是随机向量的情形。独立性的直观意义是:
)是随机向量的情形。独立性的直观意义是: 中的任何一个取值的概率规律,并不随其中的其他随机变量取什么值而改变。在实际问题中通常用它来表征多个独立操作的随机试验结果或多种有独立来源的随机因素的概率特性,因此它对于概率统计的应用是十分重要的。
中的任何一个取值的概率规律,并不随其中的其他随机变量取什么值而改变。在实际问题中通常用它来表征多个独立操作的随机试验结果或多种有独立来源的随机因素的概率特性,因此它对于概率统计的应用是十分重要的。
从随机变量(或向量) 的独立性还可以推出:设
的独立性还可以推出:设 是
是 取值的空间中的任意波莱尔集,
取值的空间中的任意波莱尔集, 。设
。设 是独立的,则它们中的任意个都是独立的。但逆之即使其中任何
是独立的,则它们中的任意个都是独立的。但逆之即使其中任何 个是独立的,也不保证
个是独立的,也不保证 是独立的。又如果
是独立的。又如果 ,是
,是 个连续函数或初等函数(或更一般的波莱尔可测函数),则从
个连续函数或初等函数(或更一般的波莱尔可测函数),则从 的独立性可推出
的独立性可推出 也独立。如果随机变量(随机向量)序列
也独立。如果随机变量(随机向量)序列 中任何有限个都独立,则称之为独立随机变量(随机向量)序列。
关于随机变量的矩、特征函数、母函数及半不变量,分别见数学期望、方差、動差及概率分布。
中任何有限个都独立,则称之为独立随机变量(随机向量)序列。
关于随机变量的矩、特征函数、母函数及半不变量,分别见数学期望、方差、動差及概率分布。
随机变量的函数[编辑]
一个新的随机变量能被博雷尔可测函数定义  来产生一个随机变量
来产生一个随机变量 。
。 的累积分布函数是:
的累积分布函数是:

如果博雷尔函数可逆:

得到它的概率密度函数:

定义 为实数,在连续性随机变量里,让
为实数,在连续性随机变量里,让 

如果 ,那么
,那么 

如果

可以得到:

參考文獻[编辑]
- ^ 刘明忠,王雪,周陈焱主编,大学应用数学,重庆大学出版社,2021.11,第248页
外部链接[编辑]
- Hazewinkel, Michiel (编), Random variable, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
- Zukerman, Moshe, Introduction to Queueing Theory and Stochastic Teletraffic Models (PDF), 2014 [2017-03-01], (原始内容 (PDF)存档于2016-08-11)
- Zukerman, Moshe, Basic Probability Topics (PDF), 2014 [2017-03-01], (原始内容 (PDF)存档于2021-04-02)














![{\displaystyle X(S)=[a,\,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df17530074a67b7e46f3c915cff7829ece9717b2)

![{\displaystyle {\mathcal {I}}={\bigg \{}A\in {\mathcal {P}}(\mathbb {R} )\,{\bigg |}\,(\exists a)(\exists b)\left[\,(a,\,b\in \mathbb {R} )\wedge (A=(a,\,b))\,\right]{\bigg \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d0bd0ac0429611111bd22048ae71d327e7e57cb)


![{\displaystyle (-\infty ,\,r]\in {\mathcal {B}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d9e2cefbdce60da2e8821bca1926e11247a0a8b)
![{\displaystyle (r,\,\infty )=\bigcup \left\{A\in {\mathcal {I}}\,{\bigg |}\,(\exists n\in \mathbb {N} )\left[A=(r,\,n)\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c02dadb05b9092a3ca3b9807618361f38872b6a)
![{\displaystyle (-\infty ,\,r]=\mathbb {R} -(r,\,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bc762ee629f43a023a45a8cd254d44b3e91768)
![{\displaystyle (-\infty ,\,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/960a6fafe2d4ddb72b638f794620827e8d069d6c)

![{\displaystyle (-\infty ,\,b)=\bigcup \left\{A\in {\mathcal {P}}(\mathbb {R} )\,{\bigg |}\,(\exists n\in \mathbb {N} )\left[A=(-\infty ,\,b-{\frac {1}{n}}]\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b540d9f91cffaf32042c5bbd4b2012abb66485)
![{\displaystyle (a,\,b)=\left(\mathbb {R} -(-\infty ,\,a]\right)\cup (-\infty ,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65909ed0997d08904c413d8e0fbbd9827ceee25b)




























































