数值孔径

数值孔径(英語:NA, Numerical aperture)是光学系统的一个无量纲数,用以衡量该系统能够收集的光的角度范围。在光学的不同领域,数值孔径的精确定义略有不同。在光学显微镜领域,数值孔径描述了物镜收光锥角的大小,而后者决定了显微镜收光能力和空间分辨率;在光纤领域,数值孔径则描述了光进出光纤时的锥角大小。
普通光学中的数值孔径概念
[编辑]在光学领域,尤其是显微镜研究领域中,光学系统(如透镜)的数值孔径的定义为
其中n为透镜工作介质的折射率(如空气的折射率是1.0,纯水的折射率是1.33,而油类的折射率则可达到1.56)。θ则是光进出透镜时最大锥角的一半,或者可以表述为是从物在光轴上一点到光阑边缘的光线与光轴的夹角。由于数值孔径的定义中考虑了折射率的因素,因此一束光在通过平面由一种介质进入另一种时,数值孔径仍是一个常量。这一点可以从斯涅尔定律很容易地加以证明(在界面两侧是一个常数)。
在空气中,透镜的孔径角大小近似等于数值孔径的两倍(在近轴近似的条件下)。数值孔径是相对于物或像上的特定一点而言的,因此其大小也会随着该点的移动而改变。在显微学领域,如不特加注明,数值孔径一般是针对物一侧而言的。
在显微学中,透镜的数值孔径决定了其空间分辨能力,因而是非常重要的参数。光学显微镜的最高分辨能力与λ/2NA成正比,其中λ为光的波长。具有高数值孔径的透镜比具有低数值孔径者具有更高的分辨空间细节的能力。对于同样受限于衍射极限的光学系统而言,具有较高数值孔径者采光更多,因而成像更为明亮,但景深亦同时较浅。
值得一提的是,数值孔径还被用于在定义光盘格式中的坑径这一参数[1]。
数值孔径与焦比的关系
[编辑]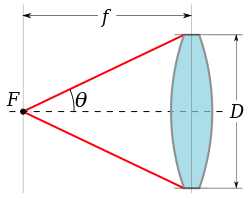
数值孔径的概念在摄影中用得较少,取而代之的是透镜的焦比这一概念。焦比一般写作 f/# 或 ,其定义为透镜的焦距与入瞳直径之比:
当透镜聚焦于无限远处时,这一比值就可以与像空间的数值孔径关联起来[2]。在右图中,透镜的数值孔径为:
因此对于在空气中使用的透镜而言(),
一般而言,上述近似在数值孔径较小的时候才成立,但一系列分析表明,对于经过良好校正的光学系统(如相机镜头)而言,这一近似即便是对较大的数值孔径也成立。对此鲁道夫·京斯莱克做出了如下解释,“认为[ ]等于 ,而非 ,这是一个普遍性的错误想法……如果主平面在实际中真的是平面,那这当然没错;但关于阿贝正弦条件的完备理论表明,当透镜已经针对彗形像差和球面像差进行过校正(所有好的摄影机镜头都应当做到这一点),这时透镜的第二主平面就不再是平面,而成为了以焦点为圆心,以焦距为半径的圆的一部分……”[3]从这种意义上来说,传统的薄透镜定义和焦比的图示就显得有些误导性了,用数值孔径来定义反倒更有意义一些。
工作焦比(有效焦比)
[编辑]焦比描述的是在物方的边缘光线与光轴接近平行的条件下,透镜接受光的能力。摄影时的情形常常满足这种条件——即被摄物与摄影机相距较远。但二者相距较近时,被摄物所成的像将不再出现在透镜的焦平面上,而焦比此时也已不能准确描述透镜的收光能力和像方的数值孔径大小(即数值孔径与焦比的近似关系不成立)。在这种情况下,像方的数值孔径就应用所谓的“工作焦比”或“有效焦比”来描述。工作焦比的定义与焦比类似,但引入了表示物像放大的校正因子:
其中, 即工作焦比, 为透镜对特定物的放大倍数,而NA则仍由边缘光线与光轴的夹角定义[2][4] 。一般而言此处的 取负值,但在摄影术领域,有时将该校正因子写作 , 取其绝对值。无论哪一种情形,该校正因子均大于或等于1。
反过来,物方的数值孔径的放大校正因子则是:
激光物理中的数值孔径概念
[编辑]在激光物理领域,数值孔径的定义略有不同。激光光束在传播过程中,发生角度很小的发散。在远离光束最窄点的地方,光束的发散程度与传播距离大致呈线性关系——相当于光束在“远场”形成了一个圆锥。在这种情形下,数值孔径的定义仍然是:
但θ的定义则与之前所述不同。激光光束的并不是一个因受到光阑限制而产生的锐利圆锥,而是一个辐照度随着离光束中心距离而逐渐降低的高斯光束。针对这种情况,激光物理学家们选择用光束的发散程度来定义θ,也就是θ由光的传播方向,以及辐照度降低到波前总辐照度1/e2时距光束中轴的距离决定。对于高斯激光束,其数值孔径与激光最小束斑尺寸有关(其数值孔径表示激光的发散程度,激光发散程度与激光最小光束直径有关):
其中是激光在真空中的波长,是光束最窄处的束斑直径(相当于辐照度衰减到1/e2时的全宽)。这意味着聚焦在小束斑上的激光会很快发散,而束斑直径较大的激光则能在很长的传播距离中几乎保持直径不变。
光纤光学中的数值孔径概念
[编辑]
在多模光纤中,只有沿着特定锥角(也就是所谓受光锥角)进入光纤的光线才能沿着光纤传播。该锥角的半角即被称为受光角 θmax。对于突变型多模光纤,受光角的大小仅取决于光纤核心与外部包覆层的折射率:
其中,n1 是光纤核心的折射率,n2 则是包覆层的折射率。尽管更高角度的光也能进入核心层,但这些光是无法在两层之间的界面上发生全反射的,因而也无法通过光纤传播。
该公式可证明如下。当一束光沿着最大受光角从折射率为n的介质中进入折射率为n1 的光纤核心层中时,由斯涅尔定律可知
几何上,
其中,是全内反射的临界角。
用cos θc 代替 sin θr,则斯涅尔定律写作:
等号两侧分别平方:
就得到前面所述的结果:
由于等式左侧的形式与数值孔径的定义形式相近,因此一般也用此式来定义各种类型光纤的数值孔径:
应该注意的是,此处n1 指的是沿着光纤中轴方向的折射率。在这种定义下,光纤的数值孔径与受光角就不是严格相等,而只是近似相等了。尤其对于单模光纤来说更是如此(单模光纤的受光角不能由折射率简单推算,因此制造商提供的数值孔径与实际受光角可能相差甚大)。
参见
[编辑]参考文献
[编辑]- ^ "High-def Disc Update: Where things stand with HD DVD and Blu-ray" (页面存档备份,存于互联网档案馆) by Steve Kindig, Crutchfield Advisor. Accessed 2008-01-18.
- ^ 2.0 2.1 Greivenkamp, John E. Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. 2004. ISBN 0-8194-5294-7. p. 29.
- ^ Rudolf Kingslake. Lenses in photography: the practical guide to optics for photographers. Case-Hoyt, for Garden City Books. 1951: 97–98.
- ^ Angelo V Arecchi, Tahar Messadi, and R. John Koshel. Field Guide to Illumination. SPIE. 2007: 48. ISBN 978-0-8194-6768-3.
外部链接
[编辑]- "Microscope Objectives: Numerical Aperture and Resolution" (页面存档备份,存于互联网档案馆) by Mortimer Abramowitz and Michael W. Davidson, Molecular Expressions: Optical Microscopy Primer (website), Florida State University, April 22, 2004.
- "Basic Concepts and Formulas in Microscopy: Numerical Aperture" (页面存档备份,存于互联网档案馆) by Michael W. Davidson, Nikon MicroscopyU (website).
- "Numerical aperture" (页面存档备份,存于互联网档案馆), Encyclopedia of Laser Physics and Technology (website).
- "Numerical Aperture and Resolution" (页面存档备份,存于互联网档案馆), UCLA Brain Research Institute Microscopy Core Facilities (website), 2007.


























