金兹堡-朗道方程
金兹堡-朗道方程,或金兹堡-朗道理论,是由维塔利·金兹堡和列夫·朗道在1950年提出的一个描述超导现象的理论[1]。早期的金兹堡-朗道方程只是一个唯象的数学模型,从宏观的角度描述了第一类超导体。1957年,苏联物理学家阿列克谢·阿布里科索夫基于金兹堡-朗道理论提出了第二类超导体的概念[2]。1959年,列夫·戈尔科夫结合BCS理论,从微观角度严格证明了金兹堡-朗道理论是BCS理论的一种极限情况[3]。为了表彰金兹堡和阿布里科索夫对超导理论的贡献,他们与研究超流理论的安东尼·莱格特共同获得了2003年的诺贝尔物理学奖。
理论[编辑]
金兹堡-朗道方程是由金兹堡和朗道在朗道的二级相变理论的基础上提出的[4]。他们断言超导态可以通过一个复序参量(complex order parameter)ψ(r) 来表征。这个形似波函数的序参量测量的是超导体在低于超导转变温度Tc时的超导有序度("degree of superconducting order"),在BCS理论的框架中可以视为描述库柏对质量中心位置的单粒子波函数[5]。在临界相变点附近,超导体的自由能密度 可被展开为如下形式:
若 ,则上式化为常态下的自由能 。表示有效质量,表示有效电荷,A 是磁矢势,为磁场强度。在后续的实验中,人们发现 ( 为基本电荷)。
当自由能取极小值时可得金兹堡-朗道方程:
由 ,可推导出电流密度
分析[编辑]
如果不考虑金兹堡-朗道方程中的磁场与梯度项,方程可化为:
由于 ,当 时,自由能的最小值出现在 ,对应着非超导的普通状态。当 时,自由能的最小值出现在 ;之所以被记为 ,是因为 是在超导体内部“无穷深”处取得的这一函数值,“无穷深”意味着完全屏蔽了外表面的电磁场或电流。[6]
若已知 ,且 ,则可以计算出金兹堡-朗道方程中各个系数的表达式。使用经验方程进行估计可知:
其中 。[6]
相干长度与穿透深度[编辑]
金兹堡-朗道方程预测了超导体中两个新的特征长度。
第一个叫做超导相干长度ξ。对于T > Tc (一般相),相干长度由以下方程给出:
对于 T < Tc (超导相),相干长度由以下方程给出:
第二个叫做穿透深度λ。这个概念最初是由伦敦兄弟在他们的伦敦理论中提出的。如果使用金兹堡-朗道模型中的参数来表示,穿透深度可以写作:
其中ψ0 表示在没有电磁场的条件下序参量的平衡值。外加磁场在超导体中的指数衰减可以通过穿透深度来定义。通过计算超导电子密度恢复到其平衡值ψ0 时产生的微小扰动,我们可以确定这个指数衰减。磁场的指数衰减与高能物理中的希格斯机制是等价的。
朗道还定义了一个参数κ。κ = / 现今被称为金兹堡-朗道参数。朗道提出,第一类超导体应满足 0<κ<1/,而第二类超导体应满足κ>1/。如此一来,金兹堡-朗道理论通过定义这两个长度,就表征了所有的超导体。
解析解[编辑]
金兹堡-朗道方程可化为以下形式的非线性偏微分方程:
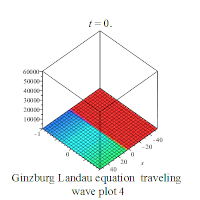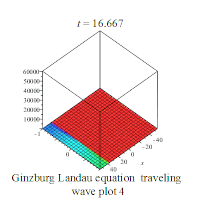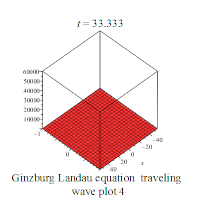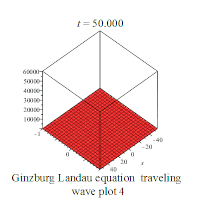
其中是一个复值函数,且有{x∈ℝ, t≥0};a和c为复常数,b∈ℝ。若假设a、b、c都是正实数,则金兹堡-朗道方程有下列行波解:
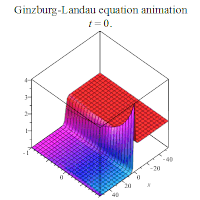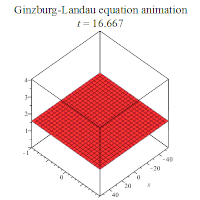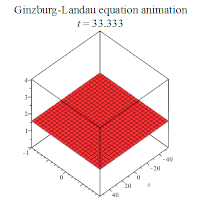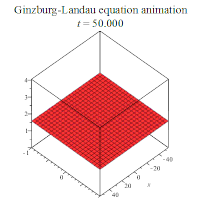
部分解析解的行为如下所示:
相关条目[编辑]
参考文献[编辑]
- ^ V. L. Ginzburg; L. D. Landau. On the Theory of Superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20: 1064. doi:10.1016/B978-0-08-010586-4.50078-X.
- ^ A.A. Abrikosov. On the Magnetic Properties of Superconductors of the Second Group. Zh.Eksp.Teor.Fiz. 1956-11, 32: 1442–1452.
- ^ L.P. Gor'kov. Microscopic derivation of the Ginzburg-Landau equations in the theory of superconductivity (PDF). Zh. Eksp. Teor. Fiz. 1959, 36: 1918–1923 [2018-01-18]. (原始内容存档 (PDF)于2018-11-23).
- ^ A.A. Abrikosov; Beknazarov. Fundamentals of the theory of metals. Amsterdam: North-Holland. 1988: 589 [2018-01-19]. ISBN 0444870946.
- ^ Neil W. Ashcroft; N. David Mermin. Solid state physics 27. repr. New York: Holt, Rinehart and Winston. 1977: 747. ISBN 0030839939.
- ^ 6.0 6.1 6.2 6.3 6.4 Tinkham, Michael. Introduction to superconductivity 2nd ed. Mineola, NY: Dover Publications. 2004: 111. ISBN 0486435032.
- ^ Inna Shingareva; Carlos Lizárraga-Celaya. Solving nonlinear partial differential equations with Maple and Mathematica. New York: Springer. 2011: 28 [2018-01-19]. ISBN 978-3-7091-0516-0. (原始内容存档于2020-08-25).
延伸阅读[编辑]
超导理论相关[编辑]
- 阿布里科索夫2003年的诺贝尔奖讲座:pdf (页面存档备份,存于互联网档案馆) 或 视频 (页面存档备份,存于互联网档案馆)
- 金兹堡2003年的诺贝尔奖讲座:pdf (页面存档备份,存于互联网档案馆) 或 视频 (页面存档备份,存于互联网档案馆)
- Neil W. Ashcroft; N. David Mermin. Solid state physics (PDF) 27. repr. New York: Holt, Rinehart and Winston. 1977: 747 [2018-01-19]. ISBN 0030839939. (原始内容 (PDF)存档于2018-01-20).
- Tinkham, Michael. Introduction to superconductivity (PDF) 2nd ed. Mineola, NY: Dover Publications. 2004: 110 [2018-01-19]. ISBN 0486435032. (原始内容存档 (PDF)于2019-05-02).
- A.A. Abrikosov; Beknazarov. Fundamentals of the theory of metals. Amsterdam: North-Holland. 1988. ISBN 0444870946.
偏微分方程相关[编辑]
- 谷超豪 《孤立子理论中的达布变换及其几何应用》 上海科学技术出版社
- 阎振亚著 《复杂非线性波的构造性理论及其应用》 科学出版社 2007年
- 李志斌编著 《非线性数学物理方程的行波解》 科学出版社
- 王东明著 《消去法及其应用》 科学出版社 2002
- 何青 王丽芬编著 《Maple 教程》 科学出版社 2010 ISBN 9787030177445
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759



































![{\displaystyle sol[1]:=u=-(1/2)*b/{\sqrt {(}}c*b)+(1/2)*{\sqrt {(}}c*b)*tanh(_{C}1+(1/4)*{\sqrt {(}}2)*{\sqrt {(}}a*b)*x/a-(3/4)*b*t)/c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e21bcdaf6e973982620d3087aaeb015c1ac6a20)
![{\displaystyle sol[2]:=u=-(1/2)*b/{\sqrt {(}}c*b)+(1/2)*{\sqrt {(}}c*b)*coth(_{C}1+(1/4)*{\sqrt {(}}2)*{\sqrt {(}}a*b)*x/a-(3/4)*b*t)/c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f210c9da3a403f1f9bb3f97e23dd4b2930a15f24)
![{\displaystyle sol[3]:=u=-(1/2*I)*b/{\sqrt {(}}-c*b)-(1/2)*{\sqrt {(}}-c*b)*tan(_{C}1+(1/4)*{\sqrt {(}}-2*a*b)*x/a-(3/4*I)*b*t)/c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51a6eb698f597c055af929e1fe67bf8cd128d603)
![{\displaystyle sol[4]:=u=-(1/2)*b/{\sqrt {(}}c*b)+(1/2)*{\sqrt {(}}c*b)*tanh(_{C}1+(1/4)*{\sqrt {(}}2)*{\sqrt {(}}a*b)*x/a-(3/4)*b*t)/c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a33c237c87e5ce078f112c65a53dc2d9f9eab641)
![{\displaystyle sol[5]:={\frac {-{\sqrt {(}}3)*exp(-1-(1/4)*{\sqrt {(}}3)*x+(9/4)*t)}{(exp(1+(1/4)*{\sqrt {(}}3)*x-(9/4)*t)+exp(-1-(1/4)*{\sqrt {(}}3)*x+(9/4)*t))}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6440d663a4e57de7308b7ce9010c5dd8c8ec64f5)