馬可夫決策過程
在數學中,馬可夫決策過程(英語:Markov decision process,MDP)是離散時間隨機控制過程。 它提供了一個數學框架,用於在結果部分隨機且部分受決策者控制的情況下對決策建模。 MDP對於研究通過動態規劃解決的最佳化問題很有用。 MDP至少早在1950年代就已為人所知;[1] 一個對馬可夫決策過程的核心研究是 羅納德·霍華德於1960年出版的《動態規劃和馬可夫過程》[2]。 它們被用於許多領域,包括機器人學,自動化,經濟學和製造業。 MDP的名稱來自俄羅斯數學家安德雷·馬可夫,因為它們是馬可夫鏈的推廣。
在每個時間步驟中,隨機過程都處於某種狀態,決策者可以選擇在狀態下可用的動作。 該隨機過程在下一時間步驟會隨機進入新狀態,並給予決策者相應的回饋。
隨機過程進入新狀態的機率受所選操作影響。 具體來說,它是由狀態轉換函數給出的。 因此,下一個狀態取決於當前狀態和決策者的動作。 但是給定和,它條件獨立於所有先前的狀態和動作; 換句話說,MDP的狀態轉換滿足马尔可夫性质。
马尔可夫决策过程是马尔可夫链的推广,不同之处在于添加了行动(允许选择)和奖励(给予动机)。反過來說,如果每个状态只存在一个操作和所有的奖励都是一样的,一个马尔可夫决策过程可以归结为一个马尔可夫链。
定义
[编辑]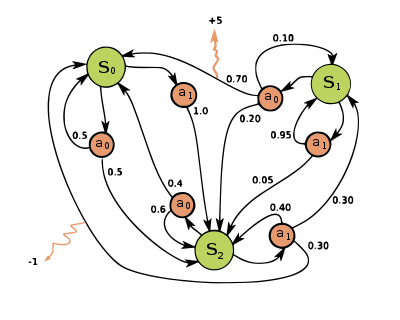
马尔可夫决策过程是一个4元组,其中:
- 是状态空间的集合,
- 是动作的集合,也被称为动作空间(比如说是状态中可用的动作集合),
- 是时刻状态下的动作导致时刻进入状态的概率,
- 状态经过动作转换到状态后收到的即时奖励(或预期的即时奖励)。
状态和行动空间可能是有限的,也可能是无限的。一些具有可数无限状态和行动空间的过程可以简化为具有有限状态和行动空间的过程。[3]
策略函数是从状态空间()到动作空间()的(潜在概率)映射。
優化目標
[编辑]马尔可夫决策过程的目标是为决策者找到一个好的“策略”:一个函数,它指定决策者在状态时将选择的动作。一旦以这种方式将马尔可夫决策过程与策略组合在一起,就可以确定在每个状态的动作,并且生成的组合行为类似于马尔可夫链(因为在状态的动作都由决定,简化为,成为一个马尔可夫轉移矩陣)。
目标是选择一个策略,使随机奖励的累积函数最大化,通常是在潜在的无限范围内的预期贴现总和:
- (我们选择也就是策略给出的动作)。并且期望值为。
其中是折现因子,满足,通常接近于1(例如,对于贴现率r,存在)。较低的折扣率促使决策者倾向于尽早采取行动,而不是无限期地推迟行动。
使上述函数最大化的策略称为最优策略,通常用表示。一个特定的MDP可能有多个不同的最佳策略。由于馬可夫決策過程的性质,可以证明最优策略是当前状态的函数,就像上面所叙述的那样。
模拟模型
[编辑]在许多情况下,很难明确地表示转移概率分布。在这种情况下,可以使用模拟器通过提供来自转换发行版的示例来隐式地对MDP建模。隐式MDP模型的一种常见形式是情景环境模拟器,它可以从初始状态启动,生成后续状态,并在每次接收到操作输入时给予奖励。通过这种方式,我们可以模拟出目标经过的状态、采取的行动以及获得的奖励(统称“轨迹”)。
另一种形式的模拟器是生成模型,即能够生成下一个状态的样本并提供所有状态和行动奖励的单步骤模拟器。[4]在用伪代码表示的算法中,通常用来表示生成模型。例如,表达式可以表示从生成模型中取样的动作,其中和是当前状态和动作,和是下一步的状态和奖励。与情景模拟器相比,生成模型的优势在于它可以从任何状态获取数据,而不仅仅是在轨迹中遇到的状态。
這些模型類形成了信息內容的層次結構:顯式模型通過從分佈中採樣簡單地生成生成模型,並且生成模型的重複應用生成軌跡模擬器。在相反的方向上,只能通過迴歸分析研究近似模型。可用於特定MDP的模型類型在確定哪種解決方案算法合適方面起著重要作用。例如,下一節中描述的動態規划算法需要一個顯式模型,而蒙地卡羅樹搜尋需要一個生成模型(或可以在任何狀態下複製的情景模擬器),而大多數強化學習算法只需要一個軌跡模擬器 。
算法
[编辑]可以通過各種方法(例如動態規劃)找到具有有限狀態和動作空間的MDP的解決方案。本節中的算法適用於具有有限狀態和動作空間並明確給出轉移概率和獎勵函數的MDP,但基本概念可以擴展到處理其他問題類別,例如使用函數趨近。
為有限狀態和動作MDP計算最優策略的標準算法系列需要存儲兩個按狀態索引的數列:第一個數列是,用來儲存實數,以及策略,用來存動作。在算法結束時,將存儲每一個狀態時的解決方案,而將存儲從狀態遵循該解決方案獲得的獎勵的折扣總和(平均)。
它們的順序取決於你所採用的算法的變體,可以一次或逐個狀態地對所有狀態執行它們,並且對某些狀態比其他狀態更頻繁。 只要沒有狀態被永久排除在任何一個步驟之外,算法最終將得出正確的解決方案。[5]
著名的變體
[编辑]數值迭代
[编辑]數值迭代也稱為反向歸納,不使用函數.相反,的值在需要時在內計算。 將的計算代入的計算得出組合步驟:
其中是迭代数,值迭代从和开始,作为价值函数的猜测。
参见
[编辑]参考文献
[编辑]- ^ Bellman, R. A Markovian Decision Process. Journal of Mathematics and Mechanics. 1957, 6 (5): 679–684 [2021-04-30]. JSTOR 24900506. (原始内容存档于2021-04-30). (页面存档备份,存于互联网档案馆)
- ^ Howard, Ronald A. Dynamic Programming and Markov Processes (PDF). The M.I.T. Press. 1960 [2021-04-30]. (原始内容存档 (PDF)于2011-10-09). (页面存档备份,存于互联网档案馆)
- ^ Wrobel, A. On Markovian Decision Models with a Finite Skeleton. Mathematical Methods of Operations Research (ZOR). 1984, 28 (February): 17–27. S2CID 2545336. doi:10.1007/bf01919083.
- ^ Kearns, Michael; Mansour, Yishay; Ng, Andrew. A Sparse Sampling Algorithm for Near-Optimal Planning in Large Markov Decision Processes. Machine Learning. 2002, 49 (193–208): 193–208. doi:10.1023/A:1017932429737
 .
.
- ^ Reinforcement Learning: Theory and Python Implementation. Beijing: China Machine Press. 2019: 44. ISBN 9787111631774.
- Yosida, K. “Functional Analysis”, Ch XIII, § 3, Springer-Verlag, 1968. ISBN 3-540-58654-7
- Ribarič.M. and I.Vidav, “An inequality for concave functions.” Glasnik Matematički 8 (28), 183–186 (1973).

















![{\displaystyle E\left[\sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/712f6adf8034f0df53957e45ab0f35441bef017e)
















