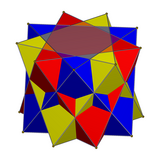
三复合正八面体
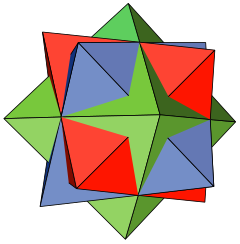 | ||
| 类别 | 复合多面体 | |
|---|---|---|
| 对偶多面体 | 三复合立方体 | |
| 性质 | ||
| 体 | 3 | |
| 面 | 24 | |
| 边 | 36 | |
| 顶点 | 18 | |
| 欧拉特征数 | F=24, E=36, V=18 (χ=6) | |
| 组成与布局 | ||
| 复合几何体数量 | 3 | |
| 复合几何体种类 | 3个正八面体 | |
| 面的种类 | 正三角形 | |
| 对称性 | ||
| 对称群 | Oh, 48阶 | |
| 旋转对称群 | O, [4,3]+, (432) | |
| 特性 | ||
| 面可递 | ||
| 图像 | ||
| ||
在几何学中,三复合正八面体是一个由3个正八面体所组成的几何结构,在这个结构中,每个正八面体都将对于其他正八面体有一个相同旋转中心的旋转关系。其最早于布鲁克纳在数学文献中提及,后来莫里兹·柯尼利斯·艾雪用此形状于1948年创作了木刻作品《群星》。
性质
[编辑]三复合正八面体是一种复合多面体,由3个正八面体组成,共具有24个面、36条边和18个顶点,正好是正八面体的三倍。[1]
结构
[编辑]正八面体可以透过将其顶点置于立方体的一对正方形面的八条棱上内接在立方体内[2]。
对于一个立方体共有三个相对面可以完成上述内嵌的动作,透过这个方式依序将三个正八面体内接在立方体内则可以构成三复合正八面体[2]。三复合正八面体中三个正八面体互相相交的棱,其相交时产生的八个顶点正好也可以构成一个立方体[3]。每组而互相相交的三条棱其交点正好将之分割成长度比为1:√2的两线段[3]。其余的八面体边成对地在立体的内部彼此相交,其交点正好将边均分为二,这意味着其交点正好位于边的中点;另外,其交角恰好为直角。
作法
[编辑]三复合正八面体可透过取三个全等的八面体,先使其重合,并以其中一个正八面体为准,并围绕着过基准正八面体之两相对顶点的对称轴旋转π/4(45度角),符合上述条件的对称轴共有三个,三个正八面体每个分别对着三轴的其中一轴旋转,即可构成三复合正八面体[4]。此外,三复合正八面体也可以对三复合立方体取对偶多面体来构造。
表面积
[编辑]一个最短边边长为a的三复合正八面体,其表面积A为[5]:
对称性
[编辑]
三复合正八面体的对称性与单一一个正八面体相同,皆为八面体群对称性[6]。其可以视为一个等边三角面多面体,这意味着其面为正三角形,具有面可递的性质,这意味着,这立体上的任意两个面A和B,透过旋转或镜射这个立体,使A移动到B原来的位置时,其面仍然占据了相同的空间区域[7]。目前已知的等边三角面多面体有一个已知的无穷序列,但已知有36种等边三角面多面体不属于这个序列,而三复合正八面体正是这36个例外之一[8]。虽三复合正八面体有面可递的性质,但由于其不具有点可递的性质因此不属于均匀多面体复合体。
在三复合正八面体中,由三个正八面体共同相交出来的区域是一个四角化六面体,其具有24个面,并可以视为在立方体的每个面上叠上四角锥的结果[3]。而四角化六面体的面皆可以与三复合正八面体的其中一个面共面,因此三复合正八面体也可以视为是一种星形四角化六面体,即四角化六面体的星形化体。另外有一种形式的四角化六面体也为等边三角面多面体,其同样是在立方体的每个面上叠上四角锥的结果,但加入的四角锥之锥高比卡塔兰立体的四角化六面体更高,使得四角锥的侧面变成正三角形(等边三角形),并形成凹多面体,其正三角形面也与三复合正八面体的面位于相同的平面上;这是另外一个已知也与三复合正八面体的面位于相同的平面上的等边三角面多面体。第三种已知也与三复合正八面体的面位于相同的平面上的几何结构是六复合正四面体,其为三复合正八面体的三个正八面体星形化成星形八面体的结果。第四种已知也与三复合正八面体的面位于相同的平面上的几何结构同样是三复合正八面体的星形化体,其排列方式与四角化六面体相同,但其加入的是倒锥体,即将立方体的面替换成向内凹陷的四角锥侧面。[8]
历史
[编辑]
在皮耶罗·德拉·弗朗西斯卡的15世纪手稿《Libellus De Quinque Corporibus Regularibus》中,德拉·弗朗西斯卡描绘了围绕着立方体内接的正八面体图形,其立方体的其中八条边分别位于正八面体的八个面上。若将三个正八面体以上述方式内接入立方体中则可以形成三复合正八面体,不过德拉·弗朗西斯卡并未描绘这种几何结构[9]。
第二次在数学文献中出现三复合正八面体是马克斯·布吕克纳于1900年的研究中,其在文献中提及了三复合正八面体并包括它的模型的照片。[3][10]
荷兰艺术家莫里兹·柯尼利斯·艾雪,在他1948年的木刻作品《群星》中使用三复合正八面体作为木刻的主要元素,其描绘了一个漂浮在太空中的三复合正八面体形状的笼子,且这个形状的笼子里有两只变色龙[11]。然而艾雪从未阅读过马克斯·布吕克纳的研究,因此被哈罗德·斯科特·麦克唐纳·考克斯特注意到,并说道:“值得注意的是,艾雪在没有任何代数或解析几何知识的情况下,能够重新发现这种高度对称的几何结构。[注 1]”,因此可以视为艾雪在布吕克纳的研究发表后又独立发现了三复合正八面体[3]。在1948年早些时候,艾雪做了一个类似主题的木刻初稿《研究星体》,不过在这个初稿中没有使用三复合正八面体,而是使用了星形四角化菱形十二面体,其虽然不是三复合正八面体,但这一种形状一定程度上与三复合正八面体相关——它可以视为三个较扁的正八面体之复合体,而这个立体有时会被称为艾雪立体。[12]这个立体拓朴结构与四角化菱形十二面体相同,皆可以视为将菱形十二面体的每个菱形面替换成菱形锥(底面为菱形的四角锥)的结果。三复合正八面体的对偶多面体是三复合立方体,其也出现于艾雪的木刻作品中,位于木刻作品《瀑布》中,星形四角化菱形十二面体旁边的立体。[11]
其他的三复合正八面体
[编辑]三个正八面体除了可以透过上述方式组合外,亦有其他组合方式,但通常会讨论具有较高对称性的形式。另一种对称性较高的三复合正八面体是将正八面体视为三角反棱柱,三个三角反棱柱可以形成具有D3d、阶数为12之对称性的均匀角柱状复合反角柱,每个三角反棱柱皆相对于其他三角反棱柱旋转了40度,其顶面可以视为是一个复合图形组成的九角星,在施莱夫利符号中可以用{9/3}或3{3}表示。[13]
注解
[编辑]- ^ 原文为:“It is remarkable that Escher, without any knowledge of algebra or analytic geometry, was able to rediscover this highly symmetrical figure.”
参见
[编辑]参考文献
[编辑]- ^ Thull. Compound of Three Octahedra. origametry.net. [2019-09-18]. (原始内容存档于2021-05-08).
- ^ 2.0 2.1 Bakos, T.; Johnson, Norman W., Octahedra inscribed in a cube, The Mathematical Gazette, 1959, 43 (343): 17–20, JSTOR 3608867
- ^ 3.0 3.1 3.2 3.3 3.4 Coxeter, H. S. M., A special book review: M. C. Escher: His life and complete graphic work, The Mathematical Intelligencer, 1985, 7 (1): 59–69, doi:10.1007/BF03023010. The discussion of the compound of three octahedra is on pp. 61–62.
- ^ Wenninger, M. J., Some interesting octahedral compounds, The Mathematical Gazette, 1968, 52 (379): 16–23, JSTOR 3614454
- ^ Weisstein, Eric W. Octahedron 3-Compound. MathWorld--A Wolfram Web Resource. [2019-09-07]. (原始内容存档于2019-09-02).
- ^ Cromwell, P.R. Polyhedra. Cambridge University Press. 1999: 363. ISBN 9780521664059. LCCN 96009420.
- ^ McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822.
- ^ 8.0 8.1 Shephard, G. C., Isohedral deltahedra, Periodica Mathematica Hungarica, 1999, 39 (1–3): 83–106, doi:10.1023/A:1004838806529.
- ^ Hart, George W., Piero della Francesca's Polyhedra, Virtual Polyhedra, 1998 [2019-09-09], (原始内容存档于2017-11-26).
- ^ Brückner, Max, Vielecke und Vielflache, Leipzig: Teubner, p. 188 and Tafel VIII 12, 1900. As cited by Coxeter (1985).
- ^ 11.0 11.1 Hart, George W., The Polyhedra of M.C. Escher, Virtual Polyhedra, 1996 [2019-09-09], (原始内容存档于2019-01-15).
- ^ The compound of three octahedra and a remarkable compound of three square dipyramids, the Escher's solid (页面存档备份,存于互联网档案馆), Livio Zefiro, University of Genova.
- ^ Skilling, John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, 79 (3): 447–457, MR 0397554, doi:10.1017/S0305004100052440