惠特尼定理概述圖 圖論 中,惠特尼定理 (英語:Whitney's theorem ),又稱為惠特尼連通性定理 (Whitney's theorem on connectivity )[1] 哈斯勒·惠特尼 於1932年[2] 2連通圖 等價性質的定理,該定理提供了關於2連通圖的不同點對之間的連通性質刻畫,描述了2連通圖的特殊性質[3]
定理陳述 [ 編輯 ] 對一個圖
G
{\displaystyle G}
G
{\displaystyle G}
G
{\displaystyle G}
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
內部不相交路徑 ,即除首尾相同(皆為
u
,
v
{\displaystyle u,v}
定理證明 [ 編輯 ] 必要性 [ 編輯 ] 因為任意兩點之間均存在路徑,於是
G
{\displaystyle G}
進一步,對於任意兩點之間有至少存在兩條內部不相交路徑,所以考慮刪除
G
{\displaystyle G}
G
{\displaystyle G}
G
{\displaystyle G}
充分性 [ 編輯 ]
G
{\displaystyle G}
u
,
v
∈
V
(
G
)
{\displaystyle u,v\in V(G)}
u
,
v
{\displaystyle u,v}
下面通過對
u
,
v
{\displaystyle u,v}
距離
d
(
u
,
v
)
{\displaystyle d(u,v)}
數學歸納法 證明:
對於
d
(
u
,
v
)
=
1
{\displaystyle d(u,v)=1}
u
v
{\displaystyle uv}
G
{\displaystyle G}
κ
(
G
)
≥
2
{\displaystyle \kappa (G)\geq 2}
惠特尼不等式 ,
λ
(
G
)
≥
κ
(
G
)
{\displaystyle \lambda (G)\geq \kappa (G)}
λ
(
G
)
≥
2
{\displaystyle \lambda (G)\geq 2}
G
{\displaystyle G}
G
{\displaystyle G}
G
−
u
v
{\displaystyle G-uv}
u
,
v
{\displaystyle u,v}
G
−
u
v
{\displaystyle G-uv}
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
假設對於
d
(
u
,
v
)
=
k
−
1
{\displaystyle d(u,v)=k-1}
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
d
(
u
,
v
)
=
k
{\displaystyle d(u,v)=k}
由於
u
,
v
{\displaystyle u,v}
k
{\displaystyle k}
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
P
{\displaystyle P}
P
{\displaystyle P}
k
{\displaystyle k}
P
{\displaystyle P}
v
{\displaystyle v}
w
{\displaystyle w}
w
{\displaystyle w}
d
(
u
,
w
)
=
k
−
1
{\displaystyle d(u,w)=k-1}
w
{\displaystyle w}
P
{\displaystyle P}
u
{\displaystyle u}
w
{\displaystyle w}
k
−
1
{\displaystyle k-1}
k
−
1
{\displaystyle k-1}
u
{\displaystyle u}
v
{\displaystyle v}
k
{\displaystyle k}
d
(
u
,
v
)
=
k
{\displaystyle d(u,v)=k}
u
,
w
{\displaystyle u,w}
u
,
w
{\displaystyle u,w}
P
,
P
′
{\displaystyle P,P'}
P
∪
P
′
{\displaystyle P\cup P'}
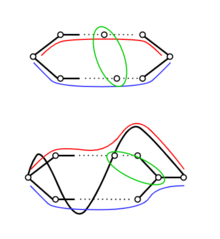
充分性的歸納證明 如果
v
∈
P
∪
P
′
{\displaystyle v\in P\cup P'}
v
{\displaystyle v}
u
{\displaystyle u}
v
{\displaystyle v}
u
{\displaystyle u}
v
{\displaystyle v}
如果
v
∉
P
∪
P
′
{\displaystyle v\notin P\cup P'}
G
{\displaystyle G}
G
−
w
{\displaystyle G-w}
u
,
v
{\displaystyle u,v}
u
,
v
{\displaystyle u,v}
Q
{\displaystyle Q}
Q
{\displaystyle Q}
P
{\displaystyle P}
P
′
{\displaystyle P'}
u
{\displaystyle u}
Q
{\displaystyle Q}
P
∪
w
v
{\displaystyle P\cup wv}
u
,
v
{\displaystyle u,v}
z
{\displaystyle z}
Q
{\displaystyle Q}
P
∪
P
′
{\displaystyle P\cup P'}
P
,
P
′
{\displaystyle P,P'}
z
{\displaystyle z}
P
{\displaystyle P}
(
u
⇝
z
)
⏟
P
∪
(
z
⇝
v
)
⏟
Q
{\displaystyle \underbrace {(u\rightsquigarrow z)} _{P}\cup \underbrace {(z\rightsquigarrow v)} _{Q}}
(
u
⇝
w
)
⏟
P
′
∪
w
v
{\displaystyle \underbrace {(u\rightsquigarrow w)} _{P'}\cup wv}
u
,
v
{\displaystyle u,v}
於是無論如何,當
d
(
u
,
v
)
=
k
{\displaystyle d(u,v)=k}
u
,
v
{\displaystyle u,v}
於是根據數學歸納法,當
G
{\displaystyle G}
u
,
v
∈
V
(
G
)
{\displaystyle u,v\in V(G)}
u
,
v
{\displaystyle u,v}
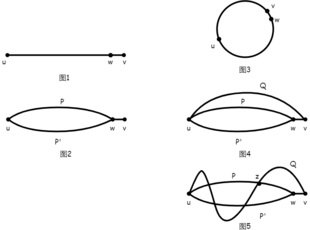
根據惠特尼定理的結論,可以得到關於2連通圖的等價描述的推論:
圖
G
{\displaystyle G}
割點 (即圖
G
{\displaystyle G}
對於圖
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
對於圖
G
{\displaystyle G}
u
,
v
{\displaystyle u,v}
G
{\displaystyle G}
C
{\displaystyle C}
u
,
v
{\displaystyle u,v}
C
{\displaystyle C}
圖
G
{\displaystyle G}
G
{\displaystyle G}
e
1
,
e
2
{\displaystyle e_{1},e_{2}}
G
{\displaystyle G}
C
{\displaystyle C}
e
1
,
e
2
{\displaystyle e_{1},e_{2}}
C
{\displaystyle C}
[4] 推論證明 [ 編輯 ] 描述1
⇔
{\displaystyle \Leftrightarrow }
描述2
⇔
{\displaystyle \Leftrightarrow }
描述4
⇔
{\displaystyle \Leftrightarrow }
u
,
v
∈
V
(
G
)
{\displaystyle u,v\in V(G)}
δ
(
G
)
≥
1
{\displaystyle \delta (G)\geq 1}
u
,
v
{\displaystyle u,v}
∃
u
x
,
v
y
∈
E
(
G
)
{\displaystyle \exists ux,vy\in E(G)}
u
x
,
v
y
{\displaystyle ux,vy}
若
u
x
∩
v
y
=
∅
{\displaystyle ux\cap vy=\varnothing }
u
x
,
v
y
{\displaystyle ux,vy}
u
x
,
v
y
{\displaystyle ux,vy}
u
,
v
{\displaystyle u,v}
若
u
x
∩
v
y
=
z
{\displaystyle ux\cap vy=z}
u
x
,
v
y
{\displaystyle ux,vy}
z
{\displaystyle z}
u
x
,
v
y
{\displaystyle ux,vy}
u
x
,
v
y
{\displaystyle ux,vy}
u
,
v
{\displaystyle u,v}
若
u
x
∩
v
y
=
u
v
{\displaystyle ux\cap vy=uv}
u
x
,
v
y
{\displaystyle ux,vy}
u
v
{\displaystyle uv}
u
v
{\displaystyle uv}
u
,
v
{\displaystyle u,v}
描述123
⇔
{\displaystyle \Leftrightarrow }
G
{\displaystyle G}
δ
(
G
)
≥
1
{\displaystyle \delta (G)\geq 1}
G
{\displaystyle G}
u
v
,
x
y
{\displaystyle uv,xy}
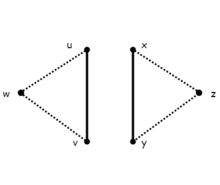
向
G
{\displaystyle G}
w
,
z
{\displaystyle w,z}
令
G
′
=
G
∪
{
w
,
z
}
∪
{
u
w
,
v
w
,
x
z
,
y
z
}
{\displaystyle G'=G\cup \{w,z\}\cup \{uw,vw,xz,yz\}}
G
′
{\displaystyle G'}
G
′
{\displaystyle G'}
G
{\displaystyle G}
G
′
{\displaystyle G'}
割集
S
{\displaystyle S}
{
w
,
z
}
{\displaystyle \{w,z\}}
S
−
{
w
,
z
}
{\displaystyle S-\{w,z\}}
G
{\displaystyle G}
G
{\displaystyle G}
|
S
|
≥
2
+
1
=
3
{\displaystyle |S|\geq 2+1=3}
|
S
|
≥
2
+
2
=
4
{\displaystyle |S|\geq 2+2=4}
{
u
,
v
,
x
,
y
}
{\displaystyle \{u,v,x,y\}}
|
S
|
≥
2
{\displaystyle |S|\geq 2}
S
{\displaystyle S}
G
{\displaystyle G}
|
S
|
≥
2
{\displaystyle |S|\geq 2}
G
′
{\displaystyle G'}
G
′
{\displaystyle G'}
k
{\displaystyle k}
expansion lemma ),它也在證明門格爾定理 中發揮了作用。[5]
那麼根據描述3,對於
G
′
{\displaystyle G'}
C
{\displaystyle C}
w
,
z
{\displaystyle w,z}
C
{\displaystyle C}
w
,
z
{\displaystyle w,z}
u
w
,
v
w
,
x
z
,
y
z
{\displaystyle uw,vw,xz,yz}
C
{\displaystyle C}
C
{\displaystyle C}
G
{\displaystyle G}
u
w
v
{\displaystyle uwv}
u
v
{\displaystyle uv}
x
z
y
{\displaystyle xzy}
x
y
{\displaystyle xy}
u
v
,
x
y
{\displaystyle uv,xy}
影響及意義 [ 編輯 ] 惠特尼定理提供了對於2連通性的更具體的性質刻畫,從而提供了另一種對於2連通性的具體證明方向。
參考文獻 [ 編輯 ]
^ Kewen Zhao. Sanya. A simple proof of Whitney's Theorem on connectivity in graphs (PDF) . Mathematica Bohemica. 2011, 136 (1): 25-26 [2021-12-10 ] . doi:10.21136/MB.2011.141446 原始內容 (PDF) 存檔於2021-12-10). ^ Hassler Whitney. Congruent graphs and the connectivity of graphs . American Journal of Mathematics. 1932, 54 (1): 150-168. doi:10.2307/2371086 ^ West, Douglas Brent. Introduction to Graph Theory . Prentice Hall. 2001: 161 . ISBN 81-7808-830-4 ^ West, Douglas Brent. Introduction to Graph Theory . Prentice Hall. 2001: 162 . ISBN 81-7808-830-4 ^ West, Douglas Brent. Introduction to Graph Theory . Prentice Hall. 2001: 162 , 167-168. ISBN 81-7808-830-4