ΔV
此條目需要補充更多來源。 (2022年8月8日) |
此條目翻譯品質不佳。 |
在天文動力學中,ΔV字面上的意思是「方向和速度的變化」。但ΔV也有其他含義,即一個用來測量軌跡變換需要多少「作用力」的純量單位,比如在改物質的軌道。
定義
[編輯]特例
[編輯]如沒有其他外力,而推力的方向是常量,可以簡化成:
這就是速度變化的大小。可是,在普遍的情況下這樣的關係不成立:假設,在時間 後常量單向加速度的方向顛倒了,那麼 , 但是ΔV跟原來的沒有顛倒推力的例子還是一樣。
在火箭的情況,「沒有其他動力」 一般來說不單是沒有大氣層的摩擦力,而是火箭發動機噴管沒有空氣靜力的向後壓力,所以「真空比沖」是用來在火箭方程中算ΔV。此外,在處理從行星表面發射時,大氣損失和重力阻力的成本被添加到ΔV預算中。[1]
產生
[編輯]ΔV一般由火箭引擎的推力提供,但也可以被其他發動機產生。ΔV的時間變化率是由發動機造成的加速度大小,即每飛船總質量的推力。通過將每質量推力添加到重力向量,和表示作用在物體上的任何其他力的向量,可以找到實際的加速度向量。
所需的總ΔV是早期設計決策的良好起點,因為對增加的複雜性的考慮被推遲到設計過程的後期。
火箭方程表明,所需的推進劑量隨着ΔV的增加而顯著增加。 因此,在現代航天器推進系統中,大量研究投入到減少給定航天飛行所需的總ΔV以及設計能夠產生更大ΔV的航天器上。
增加推進系統提供的ΔV可以通過以下方式實現:
ΔV預算
[編輯]在設計彈道時,ΔV預算被用作需要多少推進劑的良好指標。根據火箭方程,推進劑使用量是ΔV的指數函數,它還取決於排氣速度。

僅考慮飛行器在初始和最終軌道上的總能量是不可能從能量守恆中確定ΔV要求的,因為能量在排氣中被帶走(另見下文)。例如,大多數航天器在軌道上發射,其傾角相當接近發射場的緯度,以利用地球的自轉表面速度。如果出於基於任務的原因有必要將航天器置於不同傾角的軌道上,則需要相當大的ΔV,儘管最終軌道和初始軌道的比動能和勢能相等。
當火箭推力以短爆發的形式施加時,其他加速度源可以忽略不計。一次爆發的速度變化幅度可以簡單地用ΔV近似,然後可以通過添加離散燃燒所需的每個ΔV來簡單地找到要應用的總 ΔV,即使在爆發之間速度的大小和方向由於重力而變化,例如在橢圓軌道上。
有關計算ΔV的示例,請參閱霍曼轉移軌道、引力彈弓和行星際運輸網絡。同樣值得注意的是,大推力可以減少重力阻力。
將衛星保持在軌道上也需要ΔV,其也被用於推進軌道保持機動。由於大多數衛星上的推進劑負載無法補充,因此最初裝載在衛星上的推進劑量可能會很好地決定其使用壽命。
奧伯特效應
[編輯]從功率考慮,事實證明,當在速度方向上運用ΔV時,每單位ΔV獲得的特定軌道能量等於瞬時速度。 這被稱為奧伯斯效應。
例如,橢圓軌道上的衛星在高速(即低空)下加速比在低速(即高空)下加速更有效。
另一個例子是,當航天器經過一顆行星時,在最接近而不是更遠的地方燃燒推進劑會顯著提高最終速度,當行星是一個像木星一樣具有深重力場的大行星時更是如此。
另見動力彈弓。
太陽系中
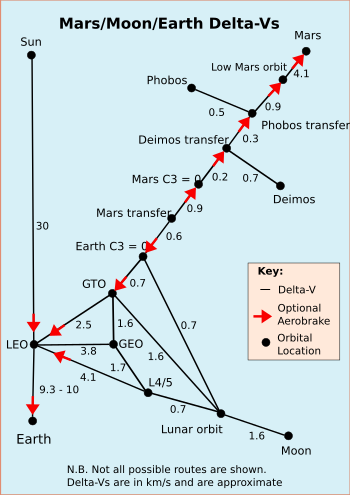
[編輯]使用常規火箭進行各種軌道機動所需的ΔV; 紅色箭頭表示可以在該特定方向執行可選大氣制動的位置,黑色數字表示適用於任一方向的以千米每秒為單位的ΔV。[2] [3]通常可以實現比所示更低的ΔV轉移,但涉及罕見的轉移窗口或需要更長的時間,見:航天動力學。
- C3:
- GEO:
- GTO:
- L4/5:
- LEO:
近地軌道再入
[編輯]例如,聯盟號飛船分兩步從國際太空站脫離軌道。 首先,它需要 2.18 米每秒的ΔV才能與空間站安全分離。 然後它需要另外128 米每秒的ΔV才能再入。[4]
參考資料
[編輯]- ^ Sarigul-Klijn, Nesrin; Noel, Chris; Sarigul-Klijn, Martinus. Air Launching Eart-to-Orbit Vehicles: Delta V gains from Launch Conditions and Vehicle Aerodynamics. 2004-01-05. ISBN 9781624100789. doi:10.2514/6.2004-872.
- ^ Rockets and Space Transportation. [June 1, 2013]. (原始內容存檔於July 1, 2007).
- ^ Delta-V Calculator. (原始內容存檔於March 12, 2000). Gives figures of 8.6 from Earth's surface to LEO, 4.1 and 3.8 for LEO to lunar orbit (or L5) and GEO resp., 0.7 for L5 to lunar orbit, and 2.2 for lunar orbit to lunar surface. Figures are said to come from Chapter 2 of Space Settlements: A Design Study 美國國會圖書館的存檔,存檔日期2001-11-28 on the NASA website [失效連結].
- ^ Gebhardt, Chris. Soyuz MS-17 safely returns three Station crewmembers to Kazakhstan. nasaspaceflight.com. nasaspaceflight.com. [10 July 2022]. (原始內容存檔於2022-08-14).