半指数函数
外观
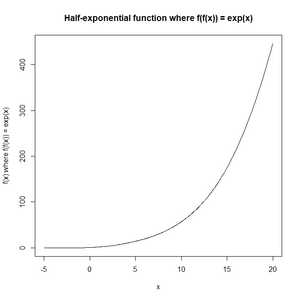
在数学上,半指数函数(Half-exponential function)是指数函数的函数平方根;换句话说,若是一个半指数函数,则与自己的复合函数会是一个指数函数:[1][2] 其中与.是常数。
解析解的不存在性
[编辑]假若以加减乘除等标准算数运算、指数、对数及实数常数等来表达一个函数,那么要不就是次指数的,要不就是超指数的,[3]因此哈代L-函数不可能是半指数函数。
建构
[编辑]有无限多的函数,其半复合函数是与彼此相同的指数函数;特别地,对于任意位于开区间当中的数及任意从映至的严格递增满射连续函数而言,都存在作为这函数扩张的严格递增连续实数函数,使得.[4],而这是以下函数方程的唯一解:
一个简单的、使得处处有连续一阶导数例子,是设且,而这会得到下式:
应用
[编辑]半指数函数出现于计算复杂性理论当中,在其中半指数成长率是介于多项式成长率与指数成长率“之间”的一种成长速率。[2]若一个函数的成长率至少与半指数函数一样快(也就是这函数与自身的复合函数的成长率是指数函数),就表示说这函数是非递减的,且对于任意而言,有。[5]
参见
[编辑]参考资料
[编辑]- ^ Kneser, H. Reelle analytische Lösungen der Gleichung φ(φ(x) = ex und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik. 1950, 187: 56–67 [2022-06-22]. MR 0035385. (原始内容存档于2022-05-18).
- ^ 2.0 2.1 Miltersen, Peter Bro; Vinodchandran, N. V.; Watanabe, Osamu. Asano, Takao; Imai, Hiroshi; Lee, D. T.; Nakano, Shin{-}Ichi; Tokuyama, Takeshi , 编. Computing and Combinatorics, 5th Annual International Conference, COCOON '99, Tokyo, Japan, July 26-28, 1999, Proceedings. Lecture Notes in Computer Science 1627. Springer: 210–220. 1999. MR 1730337. doi:10.1007/3-540-48686-0_21.
|contribution=被忽略 (帮助) - ^ van der Hoeven, J. Transseries and real differential algebra. Lecture Notes in Mathematics 1888. Springer-Verlag, Berlin. 2006. ISBN 978-3-540-35590-8. MR 2262194. doi:10.1007/3-540-35590-1.. See exercise 4.10, p. 91, according to which every such function has a comparable growth rate to an exponential or logarithmic function iterated an integer number of times, rather than the half-integer that would be required for a half-exponential function.
- ^ Crone, Lawrence J.; Neuendorffer, Arthur C. Functional powers near a fixed point. Journal of Mathematical Analysis and Applications. 1988, 132 (2): 520–529. MR 0943525. doi:10.1016/0022-247X(88)90080-7
 .
.
- ^ Razborov, Alexander A.; Rudich, Steven. Natural proofs. Journal of Computer and System Sciences. 1997, 55 (1): 24–35. MR 1473047. doi:10.1006/jcss.1997.1494
 .
.








![{\displaystyle [0,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0aa6ebe9fc37f3f23d497d0804e3d0b523ed87b5)
![{\displaystyle [A,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0a31fb8e9bf831c956c520293e98f8bf383484)


![{\displaystyle f(x)={\begin{cases}g(x)&{\mbox{if }}x\in [0,A],\\\exp g^{-1}(x)&{\mbox{if }}x\in (A,1],\\\exp f(\ln x)&{\mbox{if }}x\in (1,\infty ),\\\ln f(\exp x)&{\mbox{if }}x\in (-\infty ,0).\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e9a87e46c60296dee36e30cbf584e81636353c)




