么半範疇

張量範疇(tensor category)，或曰么半範疇 (monoidal category)， 直覺地講，是個配上張量積的阿貝爾範疇(abelian category)，可當作環的範疇化。

定義

數學中中，一個張量範疇(tensor category) (或稱幺半範疇 monoidal category) 是一個包含單一個對象的雙範疇(bicategory)。 更具體的描述：一個張量範疇是

• 一個範疇 $\mathbb C$;
• 被賦予張量積，即一個二元函子

$\otimes: \mathbb C\times\mathbb C\to\mathbb C$;

• 被賦予一個單位對象 $I$;
• 被賦予三組自然同構映射：
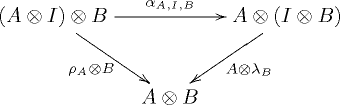
  • 結合子$\alpha$: $\alpha_{A,B,C}: (A\otimes B)\otimes C \to A\otimes(B\otimes C)$;
  • 左/右單位子: 自然同構映射 $\lambda$, $\rho$:

$\lambda_A: I\otimes A\to A$,

$\rho_A: A\otimes I\to A$;

• 滿足以下相容條件:

每$A$, $B$, $C$, $D$ $\in$ $\mathbb C$,

和

都交換.///

在這以上兩道相容條件下，任何以結合子,左右單位子和張量積組成的圖表都交換，因為 Mac Lane 凝聚定理(Mac Lane's coherence theorem): 每個幺半範疇都 幺半等價(monoidally equivalent) 於一嚴格幺半範疇（見下）.

嚴格幺半範疇

嚴格幺半範疇(strict monoidal category) 是個幺半範疇 ，其自然態射 $\alpha$, $\lambda$ 和 $\rho$ 都是恆等影射.

取任一 範疇 $\mathbb C$, 我们可構築其 自由嚴格幺半範疇 $\Sigma(\mathbb C)$:

• 對象：其每一對象是一串由$\mathbb C$裡面的對象組成之有限序列 $(A_1,\ldots, A_n$)；
• 態射：當且僅當$n=m$時，我们在二個對象 $(A_1,\ldots, A_n)$ 和 $(B_1,\ldots, B_m)$ 之間定義 態射:每 $\Sigma(\mathbb C)$-態射 是一串由 $\mathbb C$-態射組成的有限序列 $(f_1:A_1\to B_1, \ldots, f_n:A_n\to B_n)$ ；
• 張量積： 二個$\Sigma(\mathbb C)$-對象$(A_1,\ldots, A_n)$ 及 $(B_1,\ldots, B_m)$之張量積， 我们定義為 此二有限序列之串接(concatenation) $(A_1,\ldots, A_n, B_1,\ldots, B_m)$ ； 同樣地任何二 $\Sigma(\mathbb C)$-態射之張量積， 我们定義為其串接。

按：此算符 $\Sigma$ ，向由任一 範疇 $\mathbb C$ 配上 $\Sigma(\mathbb C)$，可推廣到 $\textbf{Cat}$ 上的嚴格-2-單子 (en:strict 2-monad) 。

例

取任一範疇，若以其平常範疇積作張量積，以其終對象作單位對象，則成為一個張量範疇。 亦可取任一範疇，以其餘積(co-product)作張量積，以其始對象作單位對象，亦成一個張量範疇。 （此二例實為對稱么半範疇結構。） 但亦有許多張量範疇 (例如 $R$-Mod，如下)，其張量積 既非 範疇積 亦非 範疇餘積。

以下舉張量範疇二例——向量空間範疇和集合範疇——並表明其類比：

$R$-Mod	Set
取任一域 或交換環 $R$, 各 $R$-模 所成之 範疇 $R$-模 (若R 為一域， 則 R-模即 R－向量空間) 是一 對稱么半範疇；其張量積 ⊗ 與單位對象為：$R$.	範疇 集 為一對稱么半範疇賦有張量積 × 與單位對象 {*}.
單元結合代數為$R$-模之 一對象，賦上態射 $\nabla:A\otimes A\rightarrow A$ 與 $\eta: R \rightarrow A$ 並滿足以下條件:	A 么半群 為一對象 M ，配上態射 $\circ: M \times M \rightarrow M$與 $1: \{*\} \rightarrow M$ 並滿足
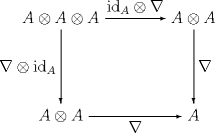and	與
.	.
A 餘代數(coalgebra) 是一個 對象 C ，被賦予 態射 $\Delta: C \rightarrow C \otimes C$ 和 $\epsilon:C\rightarrow R$ 並滿足以下條件:	集內每一對象（即每一集合）S， 都被賦予 態射 $\Delta: S \rightarrow S \times S$ 和 $\epsilon: S \rightarrow \{*\}$ 滿足以下條件:
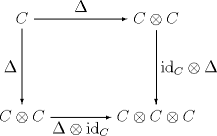
and	and
.	.
	此 ε 是唯一的，因為 $\{*\}$ （即一元集合）是個終對象.

相關的結構

• 很多張量範疇更進一步有 辮, 交換態射 or 封閉等结構. 詳見下述參考。
• 么半函子 (en:monoidal functor)為二張量範疇（么半範疇）間、保存張量積結構之函子； 么半態射為二么半函子間之態射（自然變換 (natural transformations)）。
• 一般么半群之概念可推廣成么半範疇中的么半對象(en:monoid object)。尤其者，可視一嚴格么半範疇作 範疇之「範疇」 Cat中的么半對象（並以卡氏積為么半結構）。
• 上有界交半格 構成一嚴格對稱么半範疇：其積為交，而單位元則為頂。

應用

• 么半範疇被用以定義直覺主義線性邏輯的積性部分模型。它們也是凝態物理中拓撲序的數學基礎。

• 張量範疇是二維保角場論和拓撲量子場論之代數框架.

參考

• Mac Lane, Saunders (1963). "Natural Associativity and Commutativity". Rice University Studies 49, 28–46.
• Kelly, G. Max (1964). "On MacLane's Conditions for Coherence of Natural Associativities, Commutativities, etc." Journal of Algebra 1, 397–402
• Joyal, André; Street, Ross (1993). "Braided Tensor Categories". Advances in Mathematics 102, 20–78.
• Mac Lane, Saunders (1997), Categories for the Working Mathematician (2nd ed.). New York: Springer-Verlag.
• Baez, John, Definitions
• : <<Braided Category>>, <<Encyclopaedia of Mathematics>>,Springer On-line Reference Works