三階魔方
| 此條目需要补充更多来源。 (2023年4月23日) |


三阶魔方是3×3×3的立方体结构的魔術方塊,為魔術方塊系列中最經典也是最早提出的,由匈牙利建築學教授暨雕塑家魯比克·艾爾內於1974年發明[1],最初的名稱叫Magic Cube[2],1980年Ideal Toys公司於販售此玩具,並將名稱改為Rubik's Cube[3]。
发展历史[编辑]
第一個魔方[编辑]
魯比克·厄爾諾是匈牙利的建築學和雕塑學教授,為了幫助學生們認識空間立方體的組成和結構,所以他自己動手做出了第一個魔方的雛形來,其靈感是來自於多瑙河中的沙礫[4]。
1974年,魯比克教授發明了第一個魔術方塊(當時稱作Magic Cube),並在1975年獲得匈牙利專利號HU170062,但沒有申請國際專利。第一批魔術方塊於1977年在布達佩斯的玩具店販售[5]。與Nichols的魔方不同,魯比克教授的零件是像卡榫一般互相咬合在一起,不容易因為外力而分開,而且可以以任何材質製作。
1979年九月,Ideal Toys公司將魔術方塊帶至全世界,並於1980年一、二月在倫敦、巴黎和美國的國際玩具博覽會亮相。
展出之後,Ideal Toys公司將魔術方塊的名稱改為Rubik's Cube,1980年五月,第一批魔術方塊在匈牙利出口[5]。
-
1980年,魔術方塊套裝,在匈牙利Ideal Toys公司製造的玩具。
-
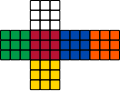
魔術方塊的色塊
流行[编辑]
魔方廣為大眾喜愛是在1980年代。從1980年到1982年,總共售出了將近200萬個魔方。1981年,一個來自英國的小男孩,派翠克·波塞特(Patrick Bossert)寫了一本名叫《你也能夠復原魔方》(ISBN 978-0-14-031483-0)的書,總共售出了將近150萬本[5]。據估計,1980年代中期,全世界有五分之一的人在玩魔術方塊[4]。
还原比賽[编辑]
根據金氏世界紀錄第一場魔方比賽於1981年3月13日,第一名是慕尼黑出生的Jury Froeschl,花了38秒。
第一個國際性的比賽於1982年6月5日在布達佩斯舉行,當時的比賽項目只有速解魔術方塊,第一名是Minh Thai,花了22.95秒,之後又逐漸增加了其他比賽規則。
- 2003年起,世界魔術方塊協會開始定期舉辦比賽,並記錄了1982年和2003年之後正式比賽的最佳成績[6]。
- 2004年,WCA使用較精準的Stackmat計時器來計時,增加比賽的準確性。
- 2007年,法國的Thibaut Jacquinot以9.86秒的成績成為首個在10秒內復原魔術方塊的人。
- 2013年,荷蘭的Mats Valk以5.55秒的成績成為當時最快復原魔術方塊的人。
- 2015年,美國高中生Collin Burns以5.253秒的成績成為當時最快復原魔術方塊的人。
- 2015年11月,美國的Lucas Etter以4.904秒的成績成為目前最快復原魔術方塊,且為首位在5秒內復原魔術方塊的的人。
- 2016年,澳洲的菲利克斯·曾姆丹格斯以4.73秒記錄成為當時最快復原魔術方塊的人。
- 2018年,澳洲的菲利克斯·曾姆丹格斯再次以4.22秒的成績,並且沒有跳步驟,亦能sub-5的成績成為當時最快復原魔術方塊的人。
- 2018年,中國的杜宇生以3.47秒的成績成為當時最快復原魔術方塊的人。
- 2023年,美國的馬克斯·朴以3.134秒的成績成為目前最快復原魔術方塊的人,領先前紀錄0.341秒
机械結構[编辑]
三階魔方由1個中心軸/核心球、6個中心塊、12個邊塊及8個角塊構成,當它們組合在一起的時候每個零件會互相牽制不會散開,並且任何一面都可水平轉動而不影響到其他方塊。三階魔方的結構不只一種,例如空心魔方。中国的一些魔方玩家,尝试对三阶魔方结构进行修改,形成适合竞速的魔方,这些修改包括对摩擦面接触方式、尺寸、重量、材质、颜色、边角处理、弹簧弹力等等的修改,这些修改都很成功,并且受到了世界魔方顶尖选手的青睐。不过这些魔方在中国以外的地区,依然会面对三阶魔方结构专利权的问题。以下是一般魔方的結構。
中心塊[编辑]

中心塊與中心軸連接在一起,但可以順著軸的方向自由地轉動。
中心塊的表面為正方形,結構略呈長方體,但長方體內側並非平面,另外中心還有一個圓柱體連接至中心軸。
從側面看,中心塊的內側會有一個圓弧狀的凹槽,組合後,中心塊和邊塊上的凹槽可組成一個圓形[7]。旋轉時,邊塊和角塊會沿著凹槽滑動。
邊塊[编辑]

邊塊的表面是兩個正方形,結構類似一個長方體從立方體的一個邊凸出來,這樣的結構可以讓邊塊嵌在兩個中心塊之間。
長方體表面上的弧度與中心塊上的弧度相同,可以沿著滑動。立方體的內側有缺角,組合後,中心塊和邊塊上的凹槽可組成一個圓形。旋轉時,邊塊和角塊會沿著凹槽滑動。另外,這個缺角還被用來固定角塊。
角塊[编辑]

角塊的表面是三個正方形,結構類似一個小立方體從立方體的一個邊凸出來,這樣的結構可以讓角塊嵌在三個邊塊之間。
與邊塊相同,小立方體的表面一樣有弧度,可以讓角塊沿著凹槽旋轉。
变化数[编辑]
三階魔方的總變化數是:
三階魔方總變化數可利用乘法原理計算,具體方法是:
- 8個角块可以互换位置(8!),也可以旋轉(3),但不能單獨翻轉一個角塊,所以总共有8!×38/3种变化状态。
- 12个边块可以互换位置(12!),也可以翻轉(2),但不能單獨翻轉一個邊塊(也就是將其兩個面對調),也不能單獨交換兩邊塊的位置,所以总共有12!×212/(2×2)种变化状态。
也就是說,拆散魔術方塊再隨意組合,有11/12的機率無法恢復原狀。(角塊或邊塊被單獨翻轉)
對於一個拆散又再隨意組合的魔術方塊,總變化數則是:
某些魔方在各个面的图案具有方向性,考虑到6个中心块各有4种朝向,但不能仅仅将一个中心块旋转90度,這時總变化数目还要再乘以46/2。此时结果为:
變體[编辑]
三階魔方也有許多變體,通常是指結構與三階魔方相同但外型不同的魔術方塊,例如粽子魔方,或外型類似但結構不同,例如空心魔方。特別地,三階魔方的許多變體是由魔術方塊愛好者改裝而來[8]。
粽子魔方[编辑]
粽子魔方,也称魔棕,是一种在三阶魔方基础之上变化而来的异形魔方。虽然外形看起来像是金字塔魔方,但两者的解法大相径庭。魔棕的解法与三阶魔方十分类似,只是由于其形状特殊而稍有不同[9]。
-
粽子魔方
空心魔方[编辑]
空心魔方由日本的冈本胜彦发明,一般以三阶为主,结构与三阶魔方不同。由于没有中心块,所以复原比三阶的难。
-
空心魔方
數獨魔方[编辑]
數獨魔方是三階魔方的另一種變體,其將九個數字貼在三階魔方表面上,遊戲規則類似數獨,要讓每個面上出現的數字不重複。數獨方塊於2006年由Jay Horowitz 在俄亥俄州發明[10]。
-
數獨魔方
Latch Cube[编辑]
Latch Cube是三階魔方的另一種變體,外型為三階魔方,但是每面上接貼有順時針或逆時針的方向箭頭,其結構類似於三階魔方,但內設有特殊卡榫,轉動時只能依面上貼的方向進行轉動。Latch Cube為著名魔方愛好者岡本勝彥發明[11]。
費雪魔方[编辑]
費雪魔方是三階魔方的另一種變體,又稱風火輪魔術方塊,是將一顆正常的三階魔方,水平旋轉45度,並且切下魔術方塊的4條稜,並貼到原本的中心塊上形成一個外觀類似三階魔方,但頂面和底面是斜線交叉的另一種魔方,由東尼·費雪於1980設計[12]。
-
Fisher's Cube
-
轉動中的費雪魔方
-
轉亂的費雪魔方
還原方法[编辑]
魔方的还原方法有很多種,以下是其中幾種常见的方法。
层先法(Layer By Layer,缩写为LBL)[编辑]
| 維基教科書中的相關電子教程:三阶魔方解法 |
這類解法分為以下幾個步驟:[a]
| 第一阶段 | 第二阶段 | 第三阶段 | 第四阶段 | 第五阶段 | 第六阶段 |
|---|---|---|---|---|---|

|

|

|

|

|

|
| 对顶层十字,还原顶层棱块。 | 还原顶层角块。 | 还原中层棱块。 | 对底层十字,还原底层棱块。 | 翻转底层角块,对齐底层颜色。 (为便于理解,此处将魔方翻转过来。) |
调整底层角块位置,还原完成。 |
角先法(Corner First)[编辑]
角先方法是先將魔方的八個角歸位定色,然後再填補棱色,最後完成復原。
棱先法[编辑]
棱先方法是先將棱塊歸位定色,然後填補底層和上層的角塊的方法。
Fridrich Method[编辑]
Fridrich Method(簡稱CFOP)其實是層先的變種,但是由於其歸納出了可能出現的各種情況,所以在記憶量上面要增大許多倍(119個公式),但同時也能有效的增加速度。其步驟分為以下幾個:
- 將底層轉出一個符合色塊分佈的十字 (Cross) 0個公式
- 同時將底層角塊和相對應棱塊歸位 (F2L,First 2 Layers) 41個公式
- 最上層利用公式將顏色統一 (OLL,Orientation of Last Layer)57個公式
- 將最上層側面的顏色統一 (PLL,Permutation of Last Layer)21個公式
桥式解法(Roux Method)[编辑]
- 先在两个侧面下方各形成正确的2X3两块,
- 使顶面的四个角块归位
- 调整中间四个棱块和侧面两个棱块的朝向
- 左右侧面顶部的棱块归位
- 中间棱块和中心块归位
记录转动的方法[编辑]

為了記錄下復原、轉亂的過程或公式的步驟,會用“辛马斯特标记”(Singmaster notation)來書寫(由大卫·辛马斯特發明)[13]。書寫方式如下:
- R(Right)、L(Left)、U(Up)、D(Down)、F(Front)、B(Back)分別代表右、左、上、下、前、後層。
- 若是順時针旋轉,則直接寫上符號;若是逆時针旋轉,則在符號後加上「'」或是「i」;若是旋轉180°,則在符號後加上「2」或是「²」。
若要更加詳細紀錄整個過程,還會使用以下符號:
- x、y、z分別代表將整個魔術方塊做R、U、F,因為在速解魔術方塊的時候,並不會總是將一個面朝向自己。
- r、l、u、d、f、b分別代表右、左、上、下、前、後兩層,代表連中間層一起轉。
- M(Middle)、E(Equator)、S(Side)代表旋轉中間層,相當於Rr'、Uu'、Bb'[14](注意x,y,z和M,E,S對應的方向不一樣)。
魔方还原世界紀錄[编辑]
截至2022年10月16日的世界紀錄:[6]
| 項目 | 紀錄 | 保持者 | 國籍 | 比賽 |
|---|---|---|---|---|
| 競速(單次) | 3.13秒 | Max Park | 美國 | Pride in Long Beach 2023 |
| 競速(平均) | 4.48秒 | Yiheng Wang(王藝衡)[15] | 中國 | Mofunland Cruise Open 2023 |
| 盲解(單次) | 12.97秒 | Tommy Cherry | 美國 | GA Cubers Personal Best Quest 2022 |
| 盲解(平均) | 15.24秒 | Tommy Cherry | 美國 | Florida Fall 2021 |
| 單手解(單次) | 6.20秒 | Max Park | 美國 | Marshall Middle Slice 2022 |
| 單手解(平均) | 8.65秒 | Patrick Ponce | 美國 | Stevenage Spring 2022 |
| 最少步數 (單次) | 16步 | Sebastiano Tronto | 意大利 | FMC 2019 |
| 最少步數 (平均) | 21.00步 | Cale Schoon | 美國 | North Star Cubing Challenge 2020 |
| 腳解(單次) | 16.96秒 | Daniel Rose-Levine | 美國 | Heartland Champs 2018 |
| 腳解(平均) | 22.22秒 | Daniel Rose-Levine | 美國 | WCA Euro 2018 |
| 多顆盲解 | 57分47秒復原65個中的62個 | Graham Siggins | 美國 | Blind Is Back LA 2022 |
注釋[编辑]
参考文献[编辑]
- ^ William Fotheringham. Fotheringham's Sporting Pastimes. Anova Books. 2007: 50. ISBN 1-86105-953-1.
- ^ 'Driven mad' Rubik's nut weeps on solving cube... after 26 years of trying (页面存档备份,存于互联网档案馆), Daily Mail Reporter, 12th January 2009.
- ^ Daintith, John. A Biographical Encyclopedia of Scientists. Bristol: Institute of Physics Pub. 1994: 771. ISBN 0-7503-0287-9.
- ^ 4.0 4.1 http://www.rubiks.com/World/Cube%20facts.aspx (页面存档备份,存于互联网档案馆)
- ^ 5.0 5.1 5.2 http://www.rubiks.com/World/Rubiks%20history.aspx. [2017-05-11]. (原始内容存档于2017-06-08). 外部链接存在于
|title=(帮助) - ^ 6.0 6.1 WCA官方紀錄. 2009-08-16 [2009-08-24]. (原始内容存档于2009-03-18).
- ^ [Media:Disassembled Rubik's cube.jpg Media:Disassembled Rubik's cube.jpg]
- ^ 林義強. 魔方改裝,啟動你的想像力. 翰林數學天地期刊, 第32期: 23-35. [2018-07-23]. (原始内容存档于2018-07-24).
- ^ 粽子魔方探讨. [2018-07-23]. (原始内容存档于2018-07-22).
- ^ US toy maker combines Sudoku and Rubik's Cube amid popularity of brain teasers. International Herald Tribune. 2007-02-17 [2008-09-30]. (原始内容存档于2008-10-15).
- ^ Latch Cube解法提示. [2018-07-23]. (原始内容存档于2016-10-04).
- ^ Tony Fisher. Tony Fisher's Rubik's Cube Type Puzzles. [2018-07-23]. (原始内容存档于2014-07-16).
- ^ Joyner, David (2002). Adventures in group theory: Rubik's Cube, Merlin's machine, and Other Mathematical Toys. Baltimore: Johns Hopkins University Press. pp. 7. ISBN 978-0-8018-6947-1.
- ^ WCA比賽規則. 2009-02-06 [2009-08-24]. (原始内容存档于2009-02-17).
- ^ Yiheng Wang (王艺衡). World Cube Association. [2023-10-19]. (原始内容存档于2023-11-14).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||