跳转到内容

伸展树

本页使用了标题或全文手工转换
维基百科，自由的百科全书
（重定向自伸展樹）
伸展树
类型树
发明时间1985年
发明者丹尼爾·斯萊托和羅伯特·塔揚
用大O符号表示的时间复杂度
算法 平均 最差
空间
搜索 均摊
插入 均摊
删除 均摊

伸展树（英語：Splay Tree）是一种能够自我平衡的二叉查找树，它能在均摊的时间内完成基于伸展（Splay）操作的插入、查找、修改和删除操作。它是由丹尼爾·斯萊托和羅伯特·塔揚在1985年发明的[1]。

在伸展树上的一般操作都基于伸展操作：假设想要对一个二叉查找树执行一系列的查找操作，为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法，在每次查找之后对树进行調整，把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

它的优势在于不需要记录用于平衡树的冗余信息。

优点

[编辑]

伸展树的自我平衡使其拥有良好的性能，因为频繁访问的节点会被移动到更靠近根节点，进而获得更快的访问速度。

  • 可靠的性能——它的平均效率不输于其他平衡树[2]。
  • 存储所需的内存少——伸展树无需记录额外的什么值来维护树的信息，相对于其他平衡树，内存占用要小。

缺点

[编辑]

伸展树最显著的缺点是它有可能会变成一条链。例如，在以非递减顺序访问全部n个之后就会出现这种情况。此时树的高度对应于最坏情况的时间效率，操作的实际时间效率可能很低。然而均摊的最坏情况是对数级的——。

即使以“只读”方式（例如通过查找操作）访问伸展树，其结构也可能会发生变化。这使得伸展树在多线程环境下会变得很复杂。具体而言，如果允许多个线程同时执行查找操作，则需要额外的维护和操作。这也使得它们不适合在纯粹的函数式编程中普遍使用，尽管用于实现优先级队列的方式不多。

操作

[编辑]

伸展(splay)

[编辑]

当一个节点x被访问过后，伸展操作会将x移动到根节点。为了进行伸展操作，我们会进行一系列的旋转，每次旋转会使x离根节点更近。通过每次访问节点后的伸展操作，最近访问的节点都会离根节点更近，且伸展树也会大致平衡，这样我们就可以得到期望均摊时间复杂度的下界——均摊。

每次旋转操作由三个因素决定：

  • x是其父节点p的左儿子还是右儿子；
  • p是否为根；
  • p是其父节点g（x的祖父节点）的左儿子还是右儿子。

在每次旋转操作后，设置p的儿子为x是很重要的。如果p为空，那么x显然就是根节点了。

共有三种旋转操作，每种都有右旋（Zig）和左旋（Zag）两种情况。为了简单起见，对每种旋转操作只展示一种情况。这些旋转操作是：

Zig：当p为根节点时进行。Zig通常只在伸展操作的最后一步进行。

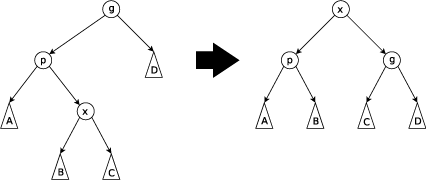
Zig-zig和Zag-zag：当p不为根节点且x和p都为左儿子或都为右儿子时进行。下图为x和p都为左儿子时的情况（即Zig-zig），需先将p右旋到g的位置，再将x右旋到p的位置。

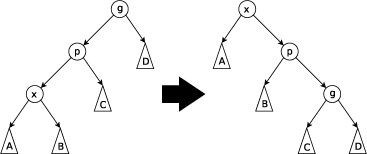
Zig-zag和Zag-zig：当p不为根节点且x为左儿子而p为右儿子时进行，反之亦然。下图为前述情况（即Zig-zag），需先将x左旋到p到的位置，再将x右旋到g的位置。

连接(join)

[编辑]

给出两棵树S和T，且S的所有元素都比T的元素要小。下面的步骤可以把它们连接成一棵树：

  • 伸展S中最大的节点。现在这个节点变为S的根节点，且没有右儿子。
  • 令T的根节点变为其右儿子。

分割(split)

[编辑]

给出一棵树和一个元素x，返回两棵树：一棵中所有的元素均小于等于x，另一棵中所有的元素大于x。下面的步骤可以完成这个操作：

  • 伸展x。这样的话x成为了这棵树的根所以它的左子树包含了所有比x小的元素，右子树包含了所有比x大的元素。
  • 把x的右子树从树中分割出来。

插入(insert)

[编辑]

插入操作是一个比较复杂的过程，具体步骤如下: 我们假定要插入的值为k。

如果当前树为空，则直接插入根。

如果当前节点的权值等于k则增加当前节点的大小并更新节点和父亲的信息，将当前节点进行splay操作。

否则按照二叉查找树的性质向下找，找到空节点就插入即可，当然在最后还要进行一次splay操作。 [3]

删除(delete)

[编辑]

令要删除的节点为x，对x进行一次splay操作将其移动到根节点的位置。

若x的大小大于1，则将x的大小减一然后结束删除操作。

否则将x删除然后执行join操作合并x的左右子树并重新指定根。


查找(find)

[编辑]

如同一般的查找树的查找方式。

实现

[编辑]

以下是伸展树的C++实现（用指针实现） 

#include <functional>

#ifndef SPLAY_TREE
#define SPLAY_TREE

template< typename T, typename Comp = std::less< T > >
class splay_tree {
private:
  Comp comp;
  unsigned long p_size;
  
  struct node {
    node *left, *right;
    node *parent;
    T key;
    node( const T& init = T( ) ) : left( 0 ), right( 0 ), parent( 0 ), key( init ) { }
  } *root;
  
  void left_rotate( node *x ) {
    node *y = x->right;
    x->right = y->left;
    if( y->left ) y->left->parent = x;
    y->parent = x->parent;
    if( x->parent ) {
        if( x == x->parent->left ) x->parent->left = y;
        else x->parent->right = y;
    }
    y->left = x;
    x->parent = y;
  }
  
  void right_rotate( node *x ) {
    node *y = x->left;
    x->left = y->right;
    if( y->right ) y->right->parent = x;
    y->parent = x->parent;
    if( x->parent ) {
        if( x == x->parent->left ) x->parent->left = y;
        else x->parent->right = y;
    }
    y->right = x;
    x->parent = y;
  }
  
  void splay( node *x ) {
    while( x->parent ) {
      if( !x->parent->parent ) {
        if( x->parent->left == x ) right_rotate( x->parent );
        else left_rotate( x->parent );
      } else if( x->parent->left == x && x->parent->parent->left == x->parent ) {
        right_rotate( x->parent->parent );
        right_rotate( x->parent );
      } else if( x->parent->right == x && x->parent->parent->right == x->parent ) {
        left_rotate( x->parent->parent );
        left_rotate( x->parent );
      } else if( x->parent->left == x && x->parent->parent->right == x->parent ) {
        right_rotate( x->parent );
        left_rotate( x->parent );
      } else {
        left_rotate( x->parent );
        right_rotate( x->parent );
      }
    }
  }
  
  void replace( node *u, node *v ) {
    if( !u->parent ) root = v;
    else if( u == u->parent->left ) u->parent->left = v;
    else u->parent->right = v;
    if( v ) v->parent = u->parent;
  }
  
  node* subtree_minimum( node *u ) {
    while( u->left ) u = u->left;
    return u;
  }
  
  node* subtree_maximum( node *u ) {
    while( u->right ) u = u->right;
    return u;
  }
public:
  splay_tree( ) : root( 0 ), p_size( 0 ) { }
  
  void insert( const T &key ) {
    node *z = root;
    node *p = 0;
    
    while( z ) {
      p = z;
      if( comp( z->key, key ) ) z = z->right;
      else z = z->left;
    }
    
    z = new node( key );
    z->parent = p;
    
    if( !p ) root = z;
    else if( comp( p->key, z->key ) ) p->right = z;
    else p->left = z;
    
    splay( z );
    p_size++;
  }
  
  node* find( const T &key ) {
    node *z = root;
    while( z ) {
      if( comp( z->key, key ) ) z = z->right;
      else if( comp( key, z->key ) ) z = z->left;
      else return z;
    }
    return 0;
  }
        
  void erase( const T &key ) {
    node *z = find( key );
    if( !z ) return;
    
    splay( z );
    
    if( !z->left ) replace( z, z->right );
    else if( !z->right ) replace( z, z->left );
    else {
      node *y = subtree_minimum( z->right );
      if( y->parent != z ) {
        replace( y, y->right );
        y->right = z->right;
        y->right->parent = y;
      }
      replace( z, y );
      y->left = z->left;
      y->left->parent = y;
    }
    
    p_size--;
  }
  
  const T& minimum( ) { return subtree_minimum( root )->key; }
  const T& maximum( ) { return subtree_maximum( root )->key; }
  
  bool empty( ) const { return root == 0; }
  unsigned long size( ) const { return p_size; }
};

#endif // SPLAY_TREE

时间效率分析

[编辑]

m次伸展操作的均摊时间效率

实际时间效率 [4]

参考来源

[编辑]
  1. ^ Sleator, Daniel D.; Tarjan, Robert E., Self-Adjusting Binary Search Trees (PDF), Journal of the ACM, 1985, 32 (3): 652–686 [2015-03-05], doi:10.1145/3828.3835, （原始内容存档 (PDF)于2015-03-05） （英语） 
  2. ^ Goodrich, Michael; Tamassia, Roberto; Goldwasser, Michael. Data Structures and Algorithms in Java 6. John Wiley & Sons, Inc. 2014: 506. ISBN 978-1-118-77133-4 （英语）. The surprising thing about splaying is that it allows us to guarantee a logarithmic amortized running time, for insertions, deletions, and searches. 
  3. ^ Splay tree - OIwiki. [2019-07-14]. （原始内容存档于2019-07-14）. 
  4. ^ Splay tree - Wikipedia. [2018-06-23]. （原始内容存档于2018-05-05）. 
检索自“https://zh.wikipedia.org/w/index.php?title=伸展树&oldid=80430599”