双二阶滤波器的传递函数有如下的形式

或

分子二项式中系数 ,
, 决定滤波器的类型:
决定滤波器的类型:
双二阶低通滤波器[编辑]

其衰减函数为[1]\[2]。

其中

-
-
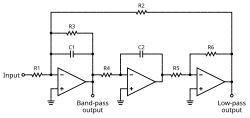
有源双二阶带通、低通滤波器电路
-
对于不同的Q值,二阶低通滤波器的衰减函数曲线
-
双二阶低通滤波器的相角
- 无源双二阶低通滤波器
无源双二阶低通滤波器由电阻、电容和电感元件组成[3]



- 有源双二阶低通滤波器
有源双二阶低通滤波器由运算放大器、电容、电感和电阻构成。
双二阶高通滤波器[编辑]
双二阶高通滤波器的传递函数为

双二阶高通滤波片的频率响应:

-
无源双二阶高通滤波器
-
双二阶高通滤波器响应图
-
双二阶高通滤波器的相角



双二阶带通滤波器[编辑]
双二阶带通滤波器的传递函数为[4]。


相角:[5]

-
双二阶无源带通滤波器
-
双二阶带通滤波器的零点和极点
-
双二阶带通滤波器频率响应
-
双二阶带通滤波器的相角



双二阶带阻滤波器[编辑]
双二阶带阻滤波器的传递函数为<refnname=rs>Rolf Schaumann,H.Xiao,M.E.van Valkenburg, p225</ref>

其频率响应

相角:

-
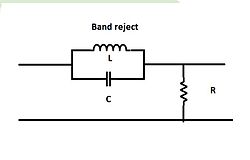
无源双二阶带阻滤波器
-
双二阶带阻滤波器的频率响应
-
双二阶带阻滤波器的相角



参考文献[编辑]
- ^ Adel S. Sedra, Peter O. Brackett, Filter Theory and Design, Active and Passive, p29,Matrix Publisher 1978
- ^ Rolf Schaumann,Haoqiao Xiao,Mac E. Van Valkenburg,Analog Filter Design, p144-148, Oxford University Press, 2013
- ^ Adel Sedra p31
- ^ Adel Sedra, p26
- ^ R.Schaumann,H.Xiao and M.Van Valkenburg, p149