莫列波紋
| 此條目需要补充更多来源。 (2022年2月5日) |
莫列波纹(英語:moiré pattern),或稱摩尔纹,是一种在数码照相机或者扫描仪等设备上,感光元件出现的高频干扰的条纹,是一种会使图片出现彩色的高频率不规则的条纹。摩爾紋因为是不规则的,所以并没有明显的形状规律。
原理[编辑]
当感光元件像素的空间频率与影像中条纹的空间频率接近时,可能产生一种新的波浪形的干扰图案,即所谓的莫列波紋。传感器的网格状纹理构成了一个这样的图案。当图案中的细条状结构与传感器的结构以小角度交叉时,这种效应也会在图像中产生明显的干扰。这种现象在一些细密纹理情况下,比如时尚摄影中的布料上,非常普遍。这种莫列波紋可能通过亮度也可能通过颜色来展现。消除这种干扰的措施匝是在传感器前使用抗混叠滤镜(也称为低通滤镜),然而这种滤镜会降低镜头的分辨率。因此,在这个问题上,必须要在莫列波紋以及分辨率之间做出取舍与妥协,不同型号相机的问题严重性不一,选择也不一样。
对于相机来说,如果设计时在镜头上安装低通滤波器会有很好效果,但会影响照片锐度;对于扫描仪来说,并无很好的方法解决。对于CRT显示器来说,指画面中出现波纹形色彩干扰的现象。主要在文字焦点突出时发生,是由于CRT显示器中电子束与荧光体碰撞时电子束的残留值影响周围荧光体引起干扰所致。通过改变焦点值可以解决这种问题。不过CRT莫列波紋是荫罩栅阴极射线管本身所固有的、内在的特质,无法完全消除,只能在一定限度内抑制减轻(如通过显示器的OSD菜单中MOIRE消除选项)。
简单地说,莫列波紋是差拍原理的一种表现。从数学上讲,两个频率接近的等幅正弦波叠加,合成信号的幅度将按照两个频率之差变化。差拍原理广泛应用到广播电视和通信中,用来变频、调制等。
同样,差拍原理也适用于空间频率。空间频率略有差异的条纹叠加,由于条纹间隔的差异、重合位置会逐渐偏移,也会形成差拍。 如果感光元件CCD/CMOS像素的空间频率与影像中条纹的空间频率接近,就会产生莫列波紋。要想消除莫列波紋,应当使镜头分辨率远小于感光元件的空间频率。当这个条件满足时,影像中不可能出现与感光元件相近的条纹,也就不会产生莫列波紋了。有些数码相机中为了减弱莫列波紋,安装有低通滤波器滤除影像中较高空间频率部分,这当然会降低图像的锐度。将来的数码相机如果像素密度能够大大提高、远远超过镜头分辨率,也不会出现莫列波紋。
字源[编辑]
莫列波紋來自法語:moiré,是一種紡織品,它的紋路類似於水波。最早這種紡織品是由絲作成,後來也用棉線或人造纖維來呈現相同的效果。
計算[编辑]
平行圖樣中的摩列[编辑]
幾何手法[编辑]
考慮兩組由平行且等距之線構成的圖樣。第一個圖樣線距為 ,第二個線距則為 ,並有 。
假如圖樣的線重疊於左側,則線之間的位移隨著往右而加大。給定數值支線以後,圖樣相反了:第二個圖樣之線位於第一個圖樣線之間。從遠距離觀察,當線重疊時看起來空白,線『倒反』時看起來暗。
第一暗區的中央在位移等於 處. 第二個圖樣第th 線與第一圖樣第th 線相比,移動了 。於是,第一暗區的中央為: 即
一暗區與一亮區之間的距離 d 為
兩暗區(同時也是兩亮區)之間距離
由此公式,易見:線距愈大,亮區與暗區之間距離越大。線距之差 愈大,亮區與暗區愈近。當然,當 ,無例外的可得一均勻灰階圖案。
數學方程手法[编辑]
於此節中我們將給出一個數學上的實例,與其中一種得出圖樣與摩列效應可以數學表示的方法。
圖案的可見性取決於其基底或介質,可能為 不透明(如紙本)或透明(如於塑膠片上)。為求討論,我們可假設兩原始圖樣皆為白紙灰階,且其列印處之不透明度由 0 (白) 至 1 (黑)之範圍給出。( 1/2 表示純灰) 任何小於0或大於1之灰階皆 "無法列印".
我們同時選擇取同位置所有圖案透明度之平均為重疊後圖案之透明度,即,和之一半,不大於1。
考慮兩幾乎一樣,正弦相關之灰階圖樣重疊“列印”。先將其一印於紙上,第二個重疊於上且座標軸對齊。我們可以
表示紙面上對一給定座標軸(舉例,x軸),對距離的正不透明度方程。
1的存在使得方程恆正,而除以2避免方程結果大於1。
為強度週期/單位距離, 表示圖樣灰階強度的週期變動。因正弦方程對 有循環,當 ,或 時,可得每強度週期(波長)之距離增長。
考慮以下週期變動有細微差異的兩圖樣:
使得 .
二方程之平均值,同時也表示重疊圖像,如下給出:
易見
且
此方程平均, ,明顯位於 [0,1]之間。有鑒於 為 與 之平均且近於兩者,摩列效應可 distinctively demonstrated by the sinusoidal envelope "拍頻"方程 , 其週期變動為 及 之差的一半( "慢"許多).
其他常見一維摩列效應包括當兩幾乎一樣之純音同時發聲時所產生的拍頻。此即在一維時間下聲音的摩列效應:原始的兩因仍在,但聽者只接收到兩者節拍之平均值與兩者頻率差之半。
本節總結:
旋轉圖樣[编辑]
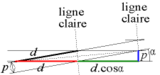
考慮兩相同線距 之圖樣,但有第二個圖樣轉動 度。從遠處看,我們可見到暗紋與亮紋:亮紋相當於節線。即,通過兩圖樣交疊處的線。
考慮"網"之單位格,易見單位格 為 菱形: 其為四邊邊長 之 平行四邊形; (我們可得一斜邊為 之三角形且 角之對邊為 ).
亮紋相當於菱形之短對角線。因對角線為鄰邊之 垂直平分線 ,易見亮紋與垂直於各圖案的線構成一等同於 的角度。
更進一步,兩亮紋之間距離為 ,長對角線之一半。長對角線唯一直角三角形之直角對邊,且直角鄰邊為 和 。 由 畢氏定理
id est
從遠處看,
- or
如 極小 (), 可做以下近似:
於是
可見, 愈小,亮紋愈遠;當兩圖樣平行時(),亮紋間距離為 "無限" (無亮紋)。
另外有給出 的兩個方法:
如果選擇測量角度,最終的誤差正比於測量誤差。選擇測量空間關係,誤差正比於空間關係的倒數。因此,對於小角度,測量空間較為理想。
意義與應用[编辑]
列印全彩圖案[编辑]
於圖像藝術與印前,列印全彩圖像需借助半色調螢幕的重疊。有些無法避免的莫列波紋是可接受的,因其十分"緊緻";即,其空間頻率高到難以察覺。有些印前作業藉由選定角度與半色調頻率來避免。莫列波紋的可見性不易預測,相同的螢幕對不同影像,成效不同。
電視螢幕與照片[编辑]
當電視中人物穿戴有特定圖樣或紋路的服裝時會產生莫列波紋。移動時莫列波紋十分易見。也是因為如此,主播或其他相關從業人員皆會注意,避免穿著造成效應的服裝。
用數位相機拍攝電視螢幕也經常有莫列波紋。電視螢幕與數位相機皆用水平掃描線捕捉影像,因此導致莫列效應。 將數位相機對電視做30度傾斜可避免效應。
海洋探勘[编辑]
莫列效應也經常用於海岸警示 (通常有關管線或纜線).[1] 莫列效應會產生指向危險的箭頭,當指示器經過危險處時,警示的箭頭在轉換方向前會先呈垂直帶狀。(50°51′21.63″N 1°19′44.77″W / 50.8560083°N 1.3291028°W).
紙鈔[编辑]
許多紙鈔採用波浪或螺線設計,以利用數位掃瞄器產生莫列圖樣的傾向防止偽造。
參考[编辑]
外部連結[编辑]
- A series of oil paintings based on Moiré principles by British artist, Pip Dickens
- A live demonstration of the Moiré effect that stems from interferences between circles (页面存档备份,存于互联网档案馆)
- An interactive example of various Moiré patterns (页面存档备份,存于互联网档案馆) Use arrow keys and mouse to manipulate layers.