格罗弗算法(英語:Grover's algorithm)是一種量子算法,於1996年由電腦科學家洛夫·格罗弗提出。假設現在有一個未知的函數,格罗弗算法只需測試此未知的函數 次,其中
次,其中 為此未知函數的定义域的大小,即可以很高的概率找到一特定的輸入值,此輸入值能使此未知函數輸出特定的值。
為此未知函數的定义域的大小,即可以很高的概率找到一特定的輸入值,此輸入值能使此未知函數輸出特定的值。
同樣的問題在經典運算下,需要至少做  次測試(因為在最壞的情況下,可能第
次測試(因為在最壞的情況下,可能第 個定義域裡的值才是正確答案)。在格罗弗發表他的算法前後,Bennett, Bernstein, Brassard, 和 Vazirani 在相近的時間證明了,任何量子算法解決此問題都最少需要對此未知的函數做
個定義域裡的值才是正確答案)。在格罗弗發表他的算法前後,Bennett, Bernstein, Brassard, 和 Vazirani 在相近的時間證明了,任何量子算法解決此問題都最少需要對此未知的函數做  次測試,因此格罗弗算法是渐进最优的。[1]
次測試,因此格罗弗算法是渐进最优的。[1]
非局域隱變量量子計算機已經被證明可以在最多 ![{\displaystyle O({\sqrt[{3}]{N}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a953364313112d7f3243feb0c59146295a65263d) 步內實現在N個條目的數據庫裡的搜索,這比格罗弗算法的
步內實現在N個條目的數據庫裡的搜索,這比格罗弗算法的  還快,然而這些搜索算法並不能使量子計算機在多項式時間內解決NP-Complete 問題。[2]
還快,然而這些搜索算法並不能使量子計算機在多項式時間內解決NP-Complete 問題。[2]
不像其他的量子算法可能會比相應的經典算法有指數級的加快,格罗弗算法二次方的加快,不過當 很大時二次方的加快也相當可觀。格罗弗算法可以在大約 264次迭代內窮舉破解一個128比特的對稱密鑰,在大約 2128次迭代內窮舉破解一個256比特的密鑰。因此,有人提倡對稱密鑰的長度應該加倍以因應未來的量子攻擊。[3]
很大時二次方的加快也相當可觀。格罗弗算法可以在大約 264次迭代內窮舉破解一個128比特的對稱密鑰,在大約 2128次迭代內窮舉破解一個256比特的密鑰。因此,有人提倡對稱密鑰的長度應該加倍以因應未來的量子攻擊。[3]
像其他的量子算法一樣,格罗弗算法是概率性的,意味著這個算法以小於1的概率給出正確答案。雖然實際上對於需要多少次重複才能給出正確的答案並沒有一個上界,但是期望的重複次數並不隨 成長。在格罗弗發表此算法的原始論文中稱此算法為數據庫搜索算法,此說法至今仍普遍。此處數據庫相當於是一張存有未知函數的所有輸出值的表,以對應的輸入值為索引。
成長。在格罗弗發表此算法的原始論文中稱此算法為數據庫搜索算法,此說法至今仍普遍。此處數據庫相當於是一張存有未知函數的所有輸出值的表,以對應的輸入值為索引。
雖然格罗弗算法的用處一直被認為是數據庫搜索,但是它也可以被認為是函數取反。
考虑一个有N个元素的无序数据集,我们设函数 。我们假设,在所有的下标x中,有且仅有一个下标x有
。我们假设,在所有的下标x中,有且仅有一个下标x有 ,我们记这个下标x为
,我们记这个下标x为 ,并且称
,并且称 为这个搜索问题的解。而格罗弗算法的目标便是找到下标
为这个搜索问题的解。而格罗弗算法的目标便是找到下标 。为此,我们构建一个酉算子
。为此,我们构建一个酉算子 ,如下
,如下

或者可以简写为

事实上,我们一般构建另一种酉算子 ,如下所示
,如下所示

我们一般将 作用在态矢量和
作用在态矢量和 的叠加态上,以实现相回传(Phase Kickback),具体流程如下
的叠加态上,以实现相回传(Phase Kickback),具体流程如下
![{\displaystyle {\begin{aligned}U_{f}|x\rangle |-\rangle &=U_{f}|x\rangle \left[{\frac {|0\rangle -|1\rangle }{\sqrt {2}}}\right]\\&={\begin{cases}{\frac {1}{\sqrt {2}}}(|x\rangle |1\rangle -|x\rangle |0\rangle )&{\text{for }}x=\omega \\{\frac {1}{\sqrt {2}}}(|x\rangle |0\rangle -|x\rangle |1\rangle )&{\text{for }}x\neq \omega \end{cases}}\\&=(-1)^{f(x)}|x\rangle |-\rangle \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8796b53920ca58760d11f5aa441ed140f14ee614)
与一般的 相比,
相比, 使用了一个辅助的qubit。
使用了一个辅助的qubit。
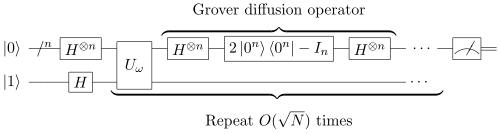 格罗弗算法的量子电路表示
格罗弗算法的量子电路表示
格罗弗算法的步骤如下
- 构建量子叠加态

- 2. 做
 次“格罗弗迭代”,具体操作如下
次“格罗弗迭代”,具体操作如下
- 将
 作用在
作用在 上
上
- 将
 作用在
作用在 上
上
- 其中,
 被称为格罗弗扩散算子
被称为格罗弗扩散算子
- 3. 测量
 ,得到求得的结果
,得到求得的结果
一般而言, 的值会很大程度上影响得到正确结果的概率,且并不是
的值会很大程度上影响得到正确结果的概率,且并不是 越大得到正确结果的概率越大。分析表明最优的
越大得到正确结果的概率越大。分析表明最优的 有
有 ,因而格罗弗算法的复杂度为
,因而格罗弗算法的复杂度为
格罗弗算法使用的技巧为振幅减枝(Amplitude amplification),实则是通过将其他态的振幅转移为解的振幅,而是在测量时使得坍塌为解的概率增加。具体如下
考虑,我们将态矢量改为以 为基,其中
为基,其中 为解。写作
为解。写作

在这种表示下,我们可以将 和
和 表示为
表示为
![{\displaystyle U_{s}:a|\omega \rangle +b|x\rangle \mapsto [|\omega \rangle \,|x\rangle ]{\begin{bmatrix}-1&0\\2/{\sqrt {N}}&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f566230cbb5089c115d3a78124976c66273512)
![{\displaystyle U_{\omega }:a|\omega \rangle +b|x\rangle \mapsto [|\omega \rangle \,|x\rangle ]{\begin{bmatrix}-1&-2/{\sqrt {N}}\\0&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d271061b669276655471fc0c72aab24928cf042a)

我们可以通过设 ,将上式改写为(所谓Jordan form)
,将上式改写为(所谓Jordan form)
 where
where 
作用r次
 则将得到
则将得到

注意到,我们的目的是区别解以及其他一般的数据,而为了达到这个目的,我们使 的振幅差别越大越好,换言之,要使得2rt和−2rt的差别足够大,便有
的振幅差别越大越好,换言之,要使得2rt和−2rt的差别足够大,便有 , 或
, 或  . 这样以来,就有
. 这样以来,就有

作用在初始态上将会有
^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\approx [|\omega \rangle \,|x\rangle ]M{\begin{bmatrix}i&0\\0&-i\end{bmatrix}}M^{-1}{\begin{bmatrix}0\\1\end{bmatrix}}=|\omega \rangle {\frac {1}{\cos(t)}}-|x\rangle {\frac {\sin(t)}{\cos(t)}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7619c5371b1e5120380587e8bfb86b10df9188e8)
简短的计算表明,格罗弗算法将具有 量级的误差.
量级的误差.

 . doi:10.1137/s0097539796300933. (原始内容存档于2016-03-06).
. doi:10.1137/s0097539796300933. (原始内容存档于2016-03-06).





![{\displaystyle O({\sqrt[{3}]{N}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a953364313112d7f3243feb0c59146295a65263d)









![{\displaystyle {\begin{aligned}U_{f}|x\rangle |-\rangle &=U_{f}|x\rangle \left[{\frac {|0\rangle -|1\rangle }{\sqrt {2}}}\right]\\&={\begin{cases}{\frac {1}{\sqrt {2}}}(|x\rangle |1\rangle -|x\rangle |0\rangle )&{\text{for }}x=\omega \\{\frac {1}{\sqrt {2}}}(|x\rangle |0\rangle -|x\rangle |1\rangle )&{\text{for }}x\neq \omega \end{cases}}\\&=(-1)^{f(x)}|x\rangle |-\rangle \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8796b53920ca58760d11f5aa441ed140f14ee614)









![{\displaystyle U_{s}:a|\omega \rangle +b|x\rangle \mapsto [|\omega \rangle \,|x\rangle ]{\begin{bmatrix}-1&0\\2/{\sqrt {N}}&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f566230cbb5089c115d3a78124976c66273512)
![{\displaystyle U_{\omega }:a|\omega \rangle +b|x\rangle \mapsto [|\omega \rangle \,|x\rangle ]{\begin{bmatrix}-1&-2/{\sqrt {N}}\\0&1\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d271061b669276655471fc0c72aab24928cf042a)








^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\approx [|\omega \rangle \,|x\rangle ]M{\begin{bmatrix}i&0\\0&-i\end{bmatrix}}M^{-1}{\begin{bmatrix}0\\1\end{bmatrix}}=|\omega \rangle {\frac {1}{\cos(t)}}-|x\rangle {\frac {\sin(t)}{\cos(t)}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7619c5371b1e5120380587e8bfb86b10df9188e8)
