
关于与“
卡诺定理 (垂线)”标题相近或相同的条目页,请见“
卡诺定理”。
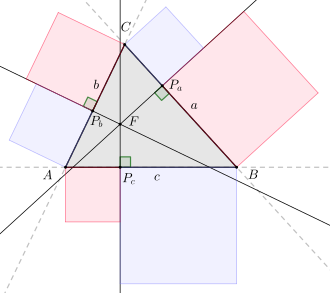 卡诺定理:若三角形三边上的垂线交于一点F,则蓝色区域面积等于红色区域面积
卡诺定理:若三角形三边上的垂线交于一点F,则蓝色区域面积等于红色区域面积
卡诺定理以拉扎尔·卡诺命名,为垂直于三角形各边的直线是否交于一点提供了一个充分必要条件。该定理也可被视为是毕氏定理的一般化。
对于一个三角形 ,其三边为
,其三边为 。考虑三条垂直于各边且交于一点的直线,若
。考虑三条垂直于各边且交于一点的直线,若 是这三条垂线在
是这三条垂线在 上的垂足,则下列关系式成立:
上的垂足,则下列关系式成立:

该命题的逆命题同样成立:若 在边上的位置满足关系式,则以这三点为垂足做出的三条垂线会交于一点。因此,该关系式为垂线是否交于一点提供了一个充分必要条件。
在边上的位置满足关系式,则以这三点为垂足做出的三条垂线会交于一点。因此,该关系式为垂线是否交于一点提供了一个充分必要条件。
若三角形 的角
的角 为直角,则可以将三条垂线的交点
为直角,则可以将三条垂线的交点 置于
置于 上。此时由于
上。此时由于 、
、  且
且 ,可得
,可得 、
、 、
、 、
、 、
、 与
与 ,代入卡诺定理的关系式后,即可推得毕氏定理
,代入卡诺定理的关系式后,即可推得毕氏定理 。
。
若三条垂线皆为中垂线,则 、
、 且
且 ,无论三边长度为何,上述关系式必会成立,故可推得三角形的三条中垂线必交于一点。
,无论三边长度为何,上述关系式必会成立,故可推得三角形的三条中垂线必交于一点。






















