线图

在图论中，图 $G$ 所对应的线图是一张能够反映 $G$ 中各边邻接性的图，记作 $L(G)$ 。简单来说， $L(G)$ 将 $G$ 中的每条边各自抽象成一个顶点；如若原图中两条边相邻，那么就给线图中对应顶点之间连接一条边。因为线图将原图的边化作了顶点，所以也可以将其视作原图的一种对偶。

哈斯勒·惠特尼证明了：假定图 $G$ 是连通的，那么除了一种特殊情况外，我们总能根据线图 $L(G)$ 的结构还原出 $G$ 的结构^[1]。以该定理为中介，可以证明线图的许多其它性质。线图总是无爪图，即线图的所有导出子图均不是 $K_{1,3}$ 。

正式定义

图 $G$ 的线图 $L(G)$ 定义如下：

$L(G)$ 的一个顶点对应 $G$ 的一边

$L(G)$ 的顶点相邻若且唯若它们在 $G$ 对应的边相邻（有公共顶点）。

该定义也可以用图论的语言表述如下：设 $G=(V,E)$ ，那么 $L(G)=(E,{\tilde {E}})$ ，且 $(e_{1},e_{2})\in {\tilde {E}}\iff e_{1}\cap e_{2}\neq \emptyset$ 。

例子

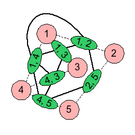
下面的例子演示了由原图生成线图的流程。

原图
制作线图的过程
结果

性质

由原图转移过来的性质

根据线图的定义，若性质／概念P仅取决于原图 $G$ 中边的邻接性，那么P便可以转移（或者说对偶）到线图 $L(G)$ 上去变成性质／概念P'，刻画线图顶点的邻接属性。例如，图 $G$ 中的一个匹配指的是图中一组不相交的边，把这一概念平移到线图上去，就等价于线图的一组不相邻的顶点——用术语来说即线图上的一个独立集。

下面就列举了原图和线图之间的若干联系：

若原图是连通的，线图也是。
若两个图同构，那么它们的线图也同构。
若 $G$ 的顶点数和边数分别为 $n$ 和 $m$ ，那么 $L(G)$ 的顶点数和边数分别是 $m$ 和 ${\textstyle \sum _{v}{\binom {\deg(v)}{2}}}$ 。
$\chi _{E}(G)=\chi _{V}(L(G))$ ，即原图的边色数等于线图的点色数。
$G$ 中的一个匹配对应了 $L(G)$ 中的一个独立集，且其大小相等。于是， $G$ 中最大匹配的大小等于 $L(G)$ 最大独立集的大小。借助这一关系，可以通过求解后者来求解前者，但反之不总是可行，因为并非所有图都能表示为某个 $G$ 的线图。在计算机科学中，最大匹配问题和最大独立集问题是两个重要的问题。前者已经被高效解决（Edmonds' Blossom Algorithm）；而后者则是NP完全问题，被普遍认为无法高效求解。
若 $G$ 存在欧拉回路，则 $L(G)$ 存在哈密顿回路，但反之不然。

惠特尼同构定理

惠特尼同构定理^[1]阐述了以下事实：设有连通图 $G_{1}$ 和 $G_{2}$ 且它们均不是三角形 $K_{3}$ 或爪形 $K_{1,3}$ 。如果 $L(G_{1})\cong L(G_{2})$ ，那么 $G_{1}\cong G_{2}$ 。也就是说，除了极特殊的情形，图 $G$ 的结构可以由线图 $L(G)$ 的结构中唯一地恢复出来。

其它性质

任何的线图都是无爪的，亦即不包含 $K_{1,3}$ 作为导出子图。因此，任意含有偶数个顶点的连通线图都存在完美匹配。

线图 $L(G)$ 的邻接矩阵 $A_{m\times m}$ 的全部特征值都不小于-2。这是因为 $A=J^{\operatorname {T} }J-2I$ ，其中 $J_{n\times m}$ 是原图 $G$ 的关联矩阵（incidence matrix）。又由于矩阵 $J^{\operatorname {T} }J$ 是半正定的，所以 $A$ 的任何特征值 $\lambda$ 均满足 $\lambda +2\geq 0$ 。