| 科学中的耦合
|
| 古典力学的耦合
|
| 转动-振动耦合(Rotational-vibrational coupling)
|
| 量子力学的耦合
|
| 转振耦合(Rovibrational coupling)
|
| 电子振动耦合(Vibronic coupling)
|
| 电子转振耦合(Rovibronic coupling)
|
| 角动量耦合(Angular momentum coupling)
|
| [[1]]
|
| 本条目存在以下问题,请协助 改善本条目或在 讨论页针对议题发表看法。
| 此条目需要 精通或熟悉相关主题的编者参与及协助编辑。 (2019年4月10日)
请邀请适合的人士改善本条目。更多的细节与详情请参见讨论页。 |
|
旋转振联(Rotational–vibrational_coupling)发生在一物体的转动频率接近其自然共振频率时。例如二个以弹簧相连的物体,以其质心为圆心旋转,同时弹簧本身周期性延展及压缩,就可能会有旋转振联的情形。
在旋转振联中,会出现角速度的振荡。当弹簧施加的力使得转动的物质靠近转动中心时,弹簧弹力(向心力)做功,使得储存在弹簧中的应变能转化为物质的动能。因此,角速度会增加。该弹簧施加的力不会一直将转动物质拉近旋转中心。旋转物质靠旋转中心越近,弹簧施加的弹力越弱,物体的速度也在增加。在某一点的物体的速度增加足够多以至于物体开始再次摆动,进入储存应变能的阶段。
在 直升机的设计中必须包含减震装置,因为在特定的角度,旋转振联会引起螺旋桨的速度振动,如果没有减振装置,振动会引起螺旋桨松动,从而导致灾难的发生。
 谐振子的恢复力与离中心的距离成正比。
谐振子的恢复力与离中心的距离成正比。
当谐振子在其原点时,系统的所有能量就转换为动能。 当谐振子离原点最远的时候,系统的所有能量都转换为势能。在谐振过程中,系统的能量在动能和势能之间来回变换。
实际的弹簧会有摩擦力。对于实际的弹簧,振动将因阻尼而变慢,最终的情况是两质量体以恒定的距离彼此相互转动,弹簧的张力恒定。
以下推导的简化条件为:不考虑弹簧本身的质量,该弹簧是理想弹簧;回复力随弹簧延展线性增加。也就是说,回复力与物体离旋转中心的距离成正比。具有这一特征的恢复力被称为简谐力(harmonic force)。
以下是位置的参数方程,时间的函数,描述旋转质量的运动:
 (1)
(1) (2)
(2)
- 符号:
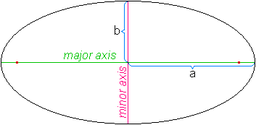
 是半长轴
是半长轴 是半短轴的一半
是半短轴的一半
该运动是时间的函数也可以看作是两种圆周运动的向量组合。 参数方程(1)和(2)可以改写为:


进行坐标变换,减去圆周运动,留下有偏心率的椭圆轨道。偏心中心位于距主轴中心 处:
处:


Category:动力系统













