環圖
在抽象代數子領域群論中,群的環圖展示了一個群的各種循環,並在小有限群的可視化中特別有用。對少於 16 個元素的群,環圖確定了群(在同構的意義下)。
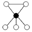
環是給定群元素 a 的冪的集合;這里的 an 是元素 a 的 n 次冪,被定義為 a 乘以自身 n 次的乘積。稱元素 a 生成了這個環。在有限群中,某個 a 的冪必定是單位元 e;最小的這種冪是環的階,即其中的不同元素的數目。在環圖中,環被表示為一系列的多邊形,頂點表示群元素,而連線指示在這個多邊形中所有元素都是同一個環的成員。
環
[編輯]環可以交疊,或者它們除了單位元之外沒有公共元素。環圖把有價值的環顯示為多邊形。
如果 a 生成 6 階環(或簡稱是 6 階的),則 a6 = e。那麼 a² 的冪的集合 {a², a4, e} 是也一個環,但這實際上沒有什麼新信息。類似的,a5 生成的環和 a 自身生成的環一樣。
所以我們只需要考慮基本的環,即不是其他環的子集的環。它們都生成自某個基本元素 a。給最初群的每個元素一個頂點。對於每個基本元素,連接 e 到 a, a 到 a², ... an-1 到 an, ... 直到回到 e。結果是環圖。
(技術上說,上述描述蘊含了如果 a² = e,a 是 2 階的(對合),它與 e 連接了兩條邊。習慣上只用一個邊。)
性質
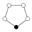
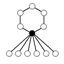
[編輯]作為群的環圖的一個例子,考慮二面體群 Dih4。下面左邊是這個群的乘法表,右邊是環圖,其中 e 指示單位元。

o e b a a2 a3 ab a2b a3b e e b a a2 a3 ab a2b a3b b b e a3b a2b ab a3 a2 a a a ab a2 a3 e a2b a3b b a2 a2 a2b a3 e a a3b b ab a3 a3 a3b e a a2 b ab a2b ab ab a b a3b a2b e a3 a2 a2b a2b a2 ab b a3b a e a3 a3b a3b a3 a2b ab b a2 a e
注意環 e, a, a², a³。它可以從乘法表中 a 的連續的冪在事實上表現如此中看出來。反轉情況也為真,換句話說: (a³)²=a², (a³)³=a 而 (a³)4=e 。這種表現對於任何群眾任何環都為真 - 環可以按任何方向游歷。

包含非素數個元素的環將隱含擁有在圖中不連接出來的環。對於上面的群 Dih4,我們可能想要在 a² 和 e 之間連線;因為 (a²)²=e;但是因為 a² 是一個更大環的一部分,我們不這麼做。
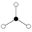
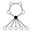
在兩個環共享非單位元的元素的時候可能有歧義。比如考慮簡單的四元群,它的環圖展示在右側。在中間行中每個元素在乘以自身的時候都得到 -1 (這里的單位元是 1)。在這種情況下我們可以使用不同顏色追蹤各個環,並且還採用對稱性處理。
如上所述,兩元素的環應該用兩條線連接,通常會縮略為一條線。
兩個不同的群可以有同樣結構的環圖,並只能通過乘積表,或依據群的基本元素標記圖中元素來區分。這個問題可能出現的最低階是下面展示的 16 階的群 Z2 x Z8 和模群的情況。(注意 - 在這些圖中有公共元素的環通過對稱性來區分。)


Z2 x Z8 的乘法表如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 |
| 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 |
| 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 |
| 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 |
| 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 |
| 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 |
從環圖中可得出的其他信息
[編輯]- 元素的逆元可以在環圖中識別出來。它是在相反的方向上有相同距離的元素。
特定群家族的圖特徵
[編輯]特定類型的群有典型的圖:
- 循環群 Zn 簡單的是一個單一的 n 邊形環,每個元素都是一個頂點。
- 在 n 是素數的時候,形如 (Zn)m 的群將有 (nm-1)/(n-1) 個 n 元素環共享單位元。
- 二面體群 Dihn 由一個 n 元素環和 n 個 2 元素環構成。
- n次對稱群,對於任何 n 階的群,n 次對稱群 Sn 都包含一個同構於這個群的子群。因此所有 n 階的群的環圖都是 Sn 的環圖的子圖。
參見
[編輯]外部連結
[編輯]- ([//web.archive.org/web/20210406013339/http://mathworld.wolfram.com/CycleGraph.html 頁面存檔備份,存於網際網路檔案館) Cycle graph article on MathWorld]
引用
[編輯]- Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.