離散傅立葉變換矩陣 是將離散傅立葉變換 以矩陣乘法來表達的一種表示式。
N 點的離散傅立葉變換可以用一個
n
×
m
{\displaystyle n\times m}
X
=
W
x
{\displaystyle X=Wx}
x
{\displaystyle x}
X
{\displaystyle X}
n
×
n
{\displaystyle n\times n}
W
{\displaystyle W}
W
=
(
ω
i
j
)
i
,
j
=
0
,
…
,
N
−
1
/
N
{\displaystyle W=(\omega ^{ij})_{i,j=0,\ldots ,N-1}/{\sqrt {N}}}
W
=
1
N
[
1
1
1
1
⋯
1
1
ω
ω
2
ω
3
⋯
ω
N
−
1
1
ω
2
ω
4
ω
6
⋯
ω
2
(
N
−
1
)
1
ω
3
ω
6
ω
9
⋯
ω
3
(
N
−
1
)
⋮
⋮
⋮
⋮
⋮
1
ω
N
−
1
ω
2
(
N
−
1
)
ω
3
(
N
−
1
)
⋯
ω
(
N
−
1
)
(
N
−
1
)
]
,
{\displaystyle W={\frac {1}{\sqrt {N}}}{\begin{bmatrix}1&1&1&1&\cdots &1\\1&\omega &\omega ^{2}&\omega ^{3}&\cdots &\omega ^{N-1}\\1&\omega ^{2}&\omega ^{4}&\omega ^{6}&\cdots &\omega ^{2(N-1)}\\1&\omega ^{3}&\omega ^{6}&\omega ^{9}&\cdots &\omega ^{3(N-1)}\\\vdots &\vdots &\vdots &\vdots &&\vdots \\1&\omega ^{N-1}&\omega ^{2(N-1)}&\omega ^{3(N-1)}&\cdots &\omega ^{(N-1)(N-1)}\\\end{bmatrix}},}
其中
ω
{\displaystyle \omega }
1
{\displaystyle 1}
n
{\displaystyle n}
primitive nth root of unity ),大小為
e
−
2
π
i
N
{\displaystyle e^{\frac {-2\pi i}{N}}}
正規化 因數
1
N
{\displaystyle {\frac {1}{\sqrt {N}}}}
ω
{\displaystyle \omega }
1
N
{\displaystyle {\frac {1}{N}}}
快速傅立葉變換 演算法利用矩陣的對稱性與W的周期性,以減少乘法所需要的時間(把計算複雜度從
O
(
N
2
)
{\displaystyle O(N^{2})}
O
(
N
log
N
)
{\displaystyle O(N\log N)}
阿達馬矩陣 和沃爾什矩陣 。
3點的離散傅立葉變換具有特殊的意義。例如:Charles LeGeyt Fortescue
兩點的離散傅立葉變換是一個很簡單的例子,其第一列代表是直流成份(總和)和第二列是交流成份(差異)。
[
1
1
1
−
1
]
/
2
{\displaystyle {\begin{bmatrix}1&1\\1&-1\end{bmatrix}}/{\sqrt {2}}}
第一列處理總和的部份,第二列處理相差的部份。
因數
1
/
2
{\displaystyle 1/{\sqrt {2}}}
四點的離散傅立葉變換矩陣如下:
1
2
[
1
1
1
1
1
−
i
(
−
i
)
2
(
−
i
)
3
1
(
−
i
)
2
(
−
i
)
4
(
−
i
)
6
1
(
−
i
)
3
(
−
i
)
6
(
−
i
)
9
]
.
{\displaystyle {\frac {1}{2}}{\begin{bmatrix}1&1&1&1\\1&-i&(-i)^{2}&(-i)^{3}\\1&(-i)^{2}&(-i)^{4}&(-i)^{6}\\1&(-i)^{3}&(-i)^{6}&(-i)^{9}\end{bmatrix}}.}
八點的離散傅立葉變換矩陣如下:
W
=
1
8
[
ω
0
ω
0
ω
0
…
ω
0
ω
0
ω
1
ω
2
…
ω
7
ω
0
ω
2
ω
4
…
ω
14
ω
0
ω
3
ω
6
…
ω
21
ω
0
ω
4
ω
8
…
ω
28
ω
0
ω
5
ω
10
…
ω
35
⋮
⋮
⋱
⋮
ω
0
ω
7
ω
14
…
ω
49
]
{\displaystyle W={\frac {1}{\sqrt {8}}}{\begin{bmatrix}\omega ^{0}&\omega ^{0}&\omega ^{0}&\ldots &\omega ^{0}\\\omega ^{0}&\omega ^{1}&\omega ^{2}&\ldots &\omega ^{7}\\\omega ^{0}&\omega ^{2}&\omega ^{4}&\ldots &\omega ^{14}\\\omega ^{0}&\omega ^{3}&\omega ^{6}&\ldots &\omega ^{21}\\\omega ^{0}&\omega ^{4}&\omega ^{8}&\ldots &\omega ^{28}\\\omega ^{0}&\omega ^{5}&\omega ^{10}&\ldots &\omega ^{35}\\\vdots &&\vdots &\ddots &\vdots \\\omega ^{0}&\omega ^{7}&\omega ^{14}&\ldots &\omega ^{49}\\\end{bmatrix}}}
其中
ω
=
e
−
2
π
i
8
=
1
2
−
i
2
{\displaystyle \omega =e^{-{\frac {2\pi i}{8}}}={\frac {1}{\sqrt {2}}}-{\frac {i}{\sqrt {2}}}}
以下用圖片來解說離散傅立葉變換的矩陣乘法概念:
圖中實部(餘弦波)是由實線代表,虛部(正弦波)由虛線代表。
最上面一行全為1,(透過乘上
1
/
8
{\displaystyle 1/{\sqrt {8}}}
fractional frequency )為−1/8倍頻率的信號。因此,這一行代表在分頻+1/8的信號強度。再下一行是8個負二次循環的複指數取樣,所以它代表-1/4倍的分頻。因此,這一行代表在分頻+1/4的信號強度。
以下總結了八點離散傅立葉變換代表的意義,依行排序,以分頻表示:
0代表直流信號成份
-1/8代表分頻為+1/8 的信號強度
-1/4代表分頻為+1/4 的信號強度
-3/8代表分頻為+3/8 的信號強度
-1/2代表分頻為+1/2 的信號強度
-5/8代表分頻為+5/8 的信號強度
-3/4代表分頻為+3/4 的信號強度
-7/8代表分頻為+7/8 的信號強度 等效上最後一行,可以當作是分頻為+1/8即代表分頻-1/8的信號強度。如此一來,則可以說這個矩陣的上面列是信號的正頻率部份的強度而下面列是信號負頻率部份的強度。
離散傅立葉變換(或可能是透過適當的尺度選擇)是一個規一化的變換,即符合能量保留(preserves energy)。可以達到規一化的合適尺度是
1
/
N
{\displaystyle 1/{\sqrt {N}}}
傅立葉變換 (帕塞瓦爾定理 )。(其他未規一化的尺度,也普遍被使用以方便計算;例如,摺積 (摺積定理 )需較簡單的形式與尺度選擇,詳述於離散傅立葉變換 條目中) 。
其他離散傅立葉變換矩陣的性質,包括其特徵值(特徵向量 ),與摺積的關係,應用等,請參見離散傅立葉變換 條目。
[ 編輯 ]
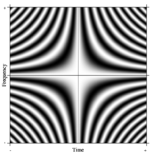
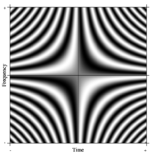
傅立葉運算實部 傅立葉運算虛部
如果我們作出一個非常大的矩陣,其中列元素為複指數(即,餘弦實部和正弦虛部),並增加解像度而不考慮邊界,我們可近似第二型Fredholm積分方程(由傅立葉運算定義連續傅立葉變換)的」核」(kernel)。此連續傅立葉變換的一部分類似於離散傅立葉變換矩陣,如圖所示。其中灰階像素值的數值是指數量。