六胞体
外观
| 部分的六胞体 | |
|---|---|
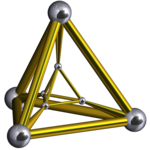 四面体柱 (四维) |
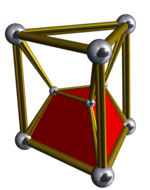 三角三角柱体柱 (四维) |
 四角锥锥 (四维) |
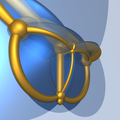 正六胞体 (五维) |
在几何学中,六胞体是指有六个胞或维面的多胞体。若六个胞都全等且都为正图形则为正六胞体。四维空间中不存在正六胞体,而在五维空间中,五维单纯形即是一种正六胞体,而六维以上的六胞体则为多维面形,一种超球面镶嵌。
四维六胞体
[编辑]在四维空间中,六胞体为由6个多面体所组成的多胞体,例如四面体柱体、三角三角柱体柱[1]和三角柱锥体。
| 名称 | 考克斯特 施莱夫利 |
胞 | 图像 | 展开图 |
|---|---|---|---|---|
| 三角三角柱体柱 | 6个三角柱 |
 |

| |
| 四面体柱体 | {3,3}×{ } t0,3{3,3,2} |
2个四面体 4个三角柱 |
 |

|
| 四角锥体锥 | 2个四角锥 4个三角锥 |
 |
五维六胞体
[编辑]在五维空间中,六胞体为由6个四维多胞体所组成的多胞体。其中,有一种正图形,即五维单纯形[2],其由6个正五胞体组成。其他的五维六胞体如五胞体锥,但其拓朴结构与正六胞体相同。拓朴结构有明显差异意味着两种无法透过移动顶点位置、扭曲或伸缩来相互变换的几何结构,例如四维的三角三角柱体柱四角锥和五维六胞体无论如何变形都无法互相变换,因此拓朴结构不同,但所有五维六胞体都可以透过扭曲来相互变换,因此在拓朴上并无明显差异。
| 名称 | 考克斯特 施莱夫利 |
胞 | 图像 | 展开图 |
|---|---|---|---|---|
| 五维正六胞体 | {3,3,3,3} |
6个正五胞体 |
 |
六维以上的六胞体
[编辑]由于六维以上的空间要形成多胞体最少要有七个胞,因此六维以上的六胞体多半是退化成超球面镶嵌(或堆砌)的图形,例如六维空间中以五维正六胞体为基底的多维面形。
参见
[编辑]参考文献
[编辑]- ^ Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).
- ^ Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
