一面體
| 部分的一面體 | |
|---|---|
 球面一面體{1,1} |
 環形一面體{4,4}1,0 |
在幾何學中,一面體是多面體的一種,是指僅由一個面構成的幾何結構。一面體在三維普通空間中是不存在的,但能存在於超球或射影平面等其他結構的空間中。
最簡單的一面體是存於球面上的幾何結構,等同於一個沒有二角形分劃的球體,更複雜地,一面體也可以是環面上的正則地區圖。在抽象幾何學中,二面體半形也是一種一面體。
一面體中並不包括任何錐體和柱體,即使是退化的形式也不存在,因為如果錐體要僅有一個面,其底面必須是零角形且不存在側面;柱體則是因為柱體有頂面和底面至少需要兩個面。
球面多面體[编辑]

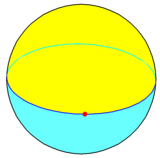
一面體可以以球面多面體的方式存在於球面或超球面上。這類一面體有兩種,一種為一面形,即由1個恰好填滿整個球面的月牙形或球弓形組成,可以視為底為一角形的多面形,在施萊夫利符號中可以用{2,1}表示[1]。這種一面體共有1個面1條稜和2個頂點,對偶多面體為一角形二面體(施萊夫利符號:{1,2})。
| 一面形 | 一面形的對偶多面體 |
|---|---|
 一面形 施萊夫利符號{2,1} |
 一角形二面體 施萊夫利符號{1,2} |
另一種一面體則以類似一角形存在於圓形上的形式存在於三維球面上,其由單個頂點在球體上,沒有邊和一個單一個面所組成。一面體的對偶是自己,即自身對偶,即可以換點和面心創造本身作為一個中心的鏡射,這種幾何結構只有1個面、沒有邊和1個頂點,在施萊夫利符號中利用{1,1}來表示。
正則地區圖[编辑]
一面體可以以正則地區圖的方式存在。
環形多面體[编辑]
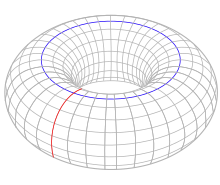

一面體可以以環形多面體的方式存在,例如{4,4}1,0[3]和{6,3}1,0[4]。其中{4,4}1,0由1個正方形組成,共有1個面、2條邊和1個頂點、{6,3}1,0由1個正方形組成,共有1個面、3條邊和2個頂點。
 {4,4}1,0 由1個面、2條稜和1個頂點組成 (v:1, e:2, f:1) |
 皮特里三面形 {6,3}1,0 由1個面、3條稜和2個頂點組成 (v:2, e:3, f:1) |
此外,以正則地區圖表達的無邊地區圖(edgeless map)也可以視為一種一面體,其施萊夫利符號表示為{0,0},由1個面、0條邊和1個頂點組成,是一個自身對偶多面體。[5]
多邊形二面體半形[编辑]
多邊形二面體半形是一種多面體半形,屬於抽象正多面體,有著多邊形二面體一半的面。其對應於圖論中的循環圖。[6]僅有偶數邊數的多邊形二面體可以存在多面體半形。2p邊形二面體半形具有1個面、p條邊和p個頂點,虧格為1,在施萊夫莉符號中可以用{2p,2}/2表示。[7][6]
| 名稱 | 圖 | χ | g | 施萊夫利符號 | 頂點 | 邊 | 面 | 群 | 階數 | 對偶多面體 | 皮特里對偶 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 二角形二面體半形[8] 二面形半形[8] |
C1 | 1 | n1 | {2,2}/2 | 1 | 1 | 1 | Dih2 | 4 | (自身對偶)[8] | 一角形二面體[8] | |
| 正方形二面體半形 | C2 | 1 | n1 | {4,2}/2 | 2 | 2 | 1 | Dih4 | 8 | 四面形半形[9] | (自身對偶)[9] | |
| 六邊形二面體半形 | C3 | 1 | n1 | {6,2}/2 | 3 | 3 | 1 | Dih6 | 12 | 六面形半形[10] | 三角形二面體[10] | |
| 八邊形二面體半形 | C4 | 1 | n1 | {8,2}/2 | 4 | 4 | 1 | Dih8 | 16 | 八面形半形[11] | (自身對偶)[11] | |
| 十邊形二面體半形 | C5 | 1 | n1 | {10,2}/2 | 5 | 5 | 1 | Dih10 | 20 | 十面形半形[12] | 五邊形二面體[12] | |
| 十二邊形二面體半形 | C6 | 1 | n1 | {12,2}/2 | 6 | 6 | 1 | Dih12 | 24 | 十二面形半形[13] | (自身對偶)[13] | |
參見[编辑]
參考文獻[编辑]
- ^ Coxeter, Introduction to geometry, 1969, Second edition, sec 21.3 Regular maps, p. 386-388
- ^ 2.0 2.1 Coxeter, H. S. M.; Moser, W. O. J., Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete 14 4th, Springer Verlag, 1980, ISBN 978-0-387-09212-6
- ^ Coxeter 1980[2], 8.3 Maps of type {4,4} on a torus.
- ^ Coxeter 1980[2], 8.4 Maps of type {3,6} or {6,3} on a torus.
- ^ The edgeless map. Regular Map database - map details. [2021-07-24]. (原始内容存档于2020-08-03).
- ^ 6.0 6.1 Séquin, Carlo. Symmetrical immersions of low-genus non-orientable regular maps (PDF). Berkeley University. [2020-08-14]. (原始内容存档 (PDF)于2015-09-23).
- ^ Regular maps in the non-orientable surface of genus 1. weddslist.com. [2020-08-14]. (原始内容存档于2019-12-28).
- ^ 8.0 8.1 8.2 8.3 The hemi-2-hosohedron. weddslist.com.
- ^ 9.0 9.1 The hemi-di-square. weddslist.com. [2020-08-14]. (原始内容存档于2020-02-01).
- ^ 10.0 10.1 The hemi-di-hexagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
- ^ 11.0 11.1 The hemi-di-octagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
- ^ 12.0 12.1 The hemi-di-decagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
- ^ 13.0 13.1 The hemi-di-dodecagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
| ||||||||||||||||||||||
