十面體
| 部分的十面體 | |
|---|---|
 正四角帳塔 |
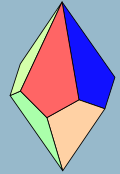 五方偏方面體 |
 八角柱 |
 雙五角錐 |
在幾何學中,十面體是指由10個面組成的多面體。在拓樸學中,有32300種不同的十面體[1],許多對稱性高的十面體通常會有五個對稱軸[2]。在幾何學上,沒有任何十面體是正十面體,也就是說找不到面由正多邊形組成且每個面全等、每個角相等的正十面體,但在抽象理論中,存在一種正十面體,半二十面體[3][4],其由十個全等的正三角形組成,但其屬於抽象多面體[5]。雖然幾何學上沒有正十面體,但仍有半正多面體,即雖面未必全部全等,但其面全部都是正多邊形且每個角等角的多面體例如正四角反稜柱和八角柱等。
常見的十面體[编辑]
所有面都由正多邊形組成且每個角都相等的十面體是半正多面體,所有十面體中僅有八角柱和正四角反稜柱符合,其中八角柱由正方形和正八邊形組成、正四角反稜柱由正方形和正三角形組成,但一般不會稱正八角柱為半正十面體。
面為正多邊形的十面體有:正八角柱、正四角帳塔、雙五角錐、側錐五角柱、側錐正二十面體欠三側錐、正四角反稜柱等[6],其中雙五角錐是三角面多面體,另外,不規則的十面體有無限多個,其中,樸拓結構有明顯差異的十面體共有32300種[1][7],其中,拓樸結構有明顯差異代表著兩種不同的多面體不能透過扭曲面或邊來改變成的多面體,例如八角柱和九角錐,但八角柱和八角錐台則沒有明顯不同的拓樸結構。
詹森多面體[编辑]
| 名稱 | 種類 | 圖像 | 編號 | 頂點 | 邊 | 面 | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|
| 正四角帳塔 | 帳塔 | 
|
J4 | 12 | 20 | 10 | 4個正三角形 5個正方形 1個正八邊形 |
C4v, [4], (*44) | 
|
| 雙正五角錐 | 雙錐體 | 
|
J13 | 7 | 15 | 10 | 10個正三角形 |
D5h, [5,2], (*225), order 20 | 
|
| 側錐五角柱 | 錐體與柱體組合 | 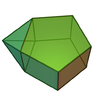
|
J52 | 11 | 19 | 10 | 4個正三角形 4個正方形 2個正五邊形 |
C2v | 
|
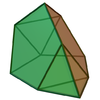
| 側錐正二十面體欠三側錐 | 切割的正二十面體 與錐體的組合 |
|
J64 | 10 | 18 | 10 | 7個正三角形 3個正五邊形 |
C3v | 
|
八角柱[编辑]

八角柱是一種底面為八邊形的柱體,是十面體的一種,由10個面24條邊和16個頂點組成[9],對偶多面體為雙八角錐[10]。正八角柱代表每個面都是正多邊形的八角柱,其每個頂點都是2個正方形和1個八邊形的公共頂點,因此具有每個角等角的性質,可以歸類為半正十面體。而頂點都是2個正方形和1個八邊形的公共頂點的這種頂角,在頂點圖中以表示。正八角柱在施萊夫利符號中可以利用{8}×{} 或 t{2, 8}來表示;在考克斯特—迪肯符号中可以利用![]()
![]()
![]()
![]()
![]() 來表示;在威佐夫符號中可以利用2 8 | 2來表示;在康威多面體表示法中可以利用P8來表示。若一個正八角柱底邊的邊長為、高為,則其體積和表面積為[11]:
來表示;在威佐夫符號中可以利用2 8 | 2來表示;在康威多面體表示法中可以利用P8來表示。若一個正八角柱底邊的邊長為、高為,則其體積和表面積為[11]:
九角錐[编辑]

九角錐是一種底面為九邊形的錐體,是十面體的一種,其由10個面、18條邊和10個頂點組成[12],對偶多面體是自己本身[13]。正九角錐是一種底面為正九邊形的九角錐。若一個正九角錐底邊的邊長為、高為,則其體積和表面積為[13]:
十面體列表[编辑]
| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|---|
| 八角柱 | 稜柱體 | 
|
t{2,8} {8}x{} |
16 | 24 | 10 | 2 | 2個八邊形 8個矩形 |
D8h, [8,2], (*822), order 32 | 
|
| 九角錐 | 稜錐體 | 
|
( )∨{9} | 10 | 18 | 10 | 2 | 1個九邊形 9個三角形 |
C9v, [9], (*99) | |
| 雙五角錐 | 雙錐體 | 
|
{ }+{5} |
7 | 15 | 10 | 2 | 10個三角形 |
D5h, [5,2], (*225), order 20 | 
|
| 四角反柱 | 反稜柱 | 
|
s{2,4} |
8 | 16 | 10 | 2 | 2個四邊形 8個三角形 |
D4d, [2+,8], (2*4), order 16 | 
|
參見[编辑]
| 维基共享资源上的相关多媒体资源:十面體 |
參考文獻[编辑]
- ^ 1.0 1.1 Steven Dutch: How Many Polyhedra are There? (页面存档备份,存于互联网档案馆)
- ^ J Phys Chem C Nanomater Interfaces. A New Mechanism of Stabilization of Large Decahedral Nanoparticles. 2012-05-31 [2016-08-21]. doi:10.1021/jp3011475. (原始内容存档于2021-12-21).
- ^ The hemi-icosahedron. [2016-08-21]. (原始内容存档于2016-08-29).
- ^ McMullen, Peter; Schulte, Egon, 6C. Projective Regular Polytopes, Abstract Regular Polytopes 1st, Cambridge University Press: 162–165, December 2002, ISBN 0-521-81496-0
- ^ N. Wedd. The hemi-icosahedron. Regular Map database. weddslist.com. 2010 [2016-08-14]. (原始内容存档于2016-08-29).
- ^ Weisstein, Eric W. (编). Decahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Counting polyhedra (页面存档备份,存于互联网档案馆) numericana.com [2016-1-10]
- ^ Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- ^ David I. McCooey. Simplest Canonical Polyhedron with D8h Symmetry: Octagonal Prism. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ David I. McCooey. Simplest Canonical Polyhedron with D8h Symmetry: Octagonal Dipyramid. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ Wolfram, Stephen. "octagon prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ David I. McCooey. Simplest Canonical Polyhedron with C9v Symmetry: Enneagonal Pyramid. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ 13.0 13.1 Wolfram, Stephen. "Enneagonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
| ||||||||||||||||||||||









