十三面體
| 部分的十三面體 | |
|---|---|
 空間填充十三面體 |
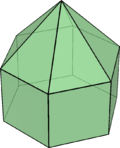 六角錐柱 |
 十一角柱 |
 四角錐反角柱 |
在幾何學中,十三面體(英語:Tridecahedron[1])是指由十三個面組成的多面體。十三面體有許多不同的拓樸形式,例如十一角柱、十二角錐,但不包含正多面體,因為找不到一個正多邊形可以組成正十三面體,正多面體只有五個[註 1][2]。
在凸十三面體中已知有177種結構屬於自身對偶多面體[註 2][3]、另外有96,262,938種不同拓樸結構的十三面體具有至少9個頂點[4],不同的拓撲結構,即他們面和頂點有不同的安排方式,使得其無法單靠扭曲或簡單地通過改變邊或面之間的長度或角度轉換成另一種多面體的多面體。
若不考慮規律性、對稱性或面是否為正多邊形或有無特殊性質的話,則十三面體有無限多種,例如:截一角十二面體、五角化一面截兩角立方體[註 3]等各種產生十三個面的組合,以此類推[註 4]。
常見的十三面體
[编辑]常見的凸十三面體有六角錐柱、四角錐反角柱、二側錐五角柱、側錐六角柱的對偶、十一角柱、十二角錐和十一角錐台等,而非嚴格凸的十三面體則有十三面形等立體。
十一角柱
[编辑]
十一角柱是一種底面為十一邊形的柱體,是十三面體的一種,其由13個面、22個頂點和33個邊組成。正十一角柱代表每個面都是正多邊形的十一角柱,其每個頂點都是2個正方形和1個十一邊形的公共頂點,頂點圖以表示,在施萊夫利符號中可以利用{11}×{} 或 t{2, 11}來表示;在考克斯特—迪肯符号中可以利用![]()
![]()
![]()
![]()
![]()
![]() 來表示;在威佐夫符號中可以利用2 11 | 2來表示;在康威多面體表示法中可以利用P11來表示。若一個正十一角柱底邊的邊長為、高為,則其體積和表面積為[5]:
來表示;在威佐夫符號中可以利用2 11 | 2來表示;在康威多面體表示法中可以利用P11來表示。若一個正十一角柱底邊的邊長為、高為,則其體積和表面積為[5]:
十二角錐
[编辑]
十二角錐是一種底面為十二邊形的錐體,是十三面體的一種,其具有13個面、24條邊和13個頂點,其對偶多面體是自己本身[6]。正十二角錐是一種底面為正十二邊形的十二角錐。若一個正十二角錐底邊的邊長為、高為,則其體積和表面積為[6]:
二側錐五角柱
[编辑]二側錐五角柱是指在五角柱的兩個四邊形側面上各疊上一個四角錐所構成的幾何體。
二側錐五角柱可以分成兩種,一種是疊上兩個四角錐相隔一個側面面,稱為間二側錐五角柱;另一種是疊上一個四角錐位於五角柱上兩相鄰的四邊形側面上,稱為鄰二側錐五角柱。其中,間二側錐五角柱是一種詹森多面體。[7]通常加入的位置能分成三種情況:「鄰」、「間」和「對」,其中「對」代表加入在相對的位置上,但「對二側錐五角柱」不存在,因為五角柱的側面沒有相對的面(五角柱中,與側面相對的元素是一條棱)。
-
鄰二側錐五角柱
-
間二側錐五角柱
十三面體列表
[编辑]| 名稱 (頂點佈局) |
符號 | 立體圖 | 展開圖 | 面 | 邊 | 頂點 | 對偶 | |
|---|---|---|---|---|---|---|---|---|
| 十一角柱 | t{2,11} {11}x{} |

|
13 | 正方形×11 十一邊形×2 |
33 | 22 | 雙十一角錐 | |
| 十二角錐 | ( )∨{12} | 
|
13 | 三角形×12 十二邊形×1 |
24 | 13 | 自身對偶 | |
| 六角錐柱 | 
|
13 | 三角形×6 正方形×6 六邊形×1 |
24 | 13 | 自身對偶 | ||
| 六角錐台錐 | 
|
13 | 三角形×6 梯形×6 六邊形×1 |
24 | 13 | |||
| 空間填充十三面體 | 
|

|
13 | 四邊形×6 五邊形×6 六邊形×1 |
30 | 19 | ||
| 四角錐反角柱 | 
|

|
13 | 三角形×12 正方形×1 |
20 | 9 | 截頂角四方偏方面體 | |
| 截頂角六方偏方面體 | 
|
13 | 1個六邊形底面 6個五邊形側面 6個鷂形側面 |
30 | 19 | 六角錐反角柱 | ||
| 間二側錐五角柱 | 
|
|
13 | 三角形×8 正方形×3 五邊形×2 |
23 | 12 | ||
| 鄰二側錐五角柱 | 
|
13 | 三角形×8 正方形×3 五邊形×2 |
23 | 12 | |||
空間填充十三面體
[编辑] | |
| 類別 | 空間填充多面體 |
|---|---|
| 對偶多面體 | 空間填充十三面體對偶 |
| 性質 | |
| 面 | 13 |
| 邊 | 30 |
| 頂點 | 19 |
| 歐拉特徵數 | F=13, E=30, V=19 (χ=2) |
| 組成與佈局 | |
| 面的種類 | 6個近似梯形 6個五邊形 1個正六邊形 |
空間填充十三面體(英語:Space-filling tridecahedron[8][9])是一種能夠完全堆滿三維空間而不留空隙的一種十三面體,具有13個面、30條邊和19個頂點。十三個面中,有六個梯形、六個五邊形和一個為正六邊形[10]。
- 空間填充十三面體的對偶多面體
其多面體的對偶多面體是一個十九面體,類似扭稜半立方體,但是其中一個頂點再進行扭稜操作前被視為一個面。
| 圖像 | 旋轉動畫 | 展開圖 | |
|---|---|---|---|
| 原本的多面體 13面體 |

|

|

|
| 對偶多面體 19面體 |

|

|
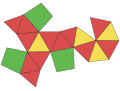
|
空間填充十三面體堆砌
[编辑]| 空間填充十三面體堆砌 | |
|---|---|
 | |
| 類型 | 等面堆砌 |
| 性質 | |
| 胞 | 十三面體 |
| 面 | 近似梯形{4} 五邊形{5} 正六邊形{6}
|
| 邊 | ∞
|
空間填充十三面體堆砌是三維空間內的一種均勻密鋪,由空間填充十三面體組成,也可以被看做是四維空間中的無限胞體,每個胞都是一個空間填充十三面體。在這個堆砌中,這些多面體胞的質心形成點集可以包含在一種由兩種菱形組成的6配位鑲嵌圖中[10]。
- 棱處相交胞
- 該堆砌的棱處相交胞為三個空間填充十三面體,頂點處相交面胞為四個空間填充十三面體。
- 棱處相交面
- 其棱處相交面皆為三個多邊形,對梯形而言,兩個底邊的棱處相交面為一個梯形和兩個五邊形,斜側邊的棱處相交面為三個四邊形,另外一個側邊的棱處相交面為一個梯形和兩個五邊形。對五邊形而言,底邊、兩個頂角側邊和其中一個下方側邊的棱處相交面也皆為一個梯形和兩個五邊形,另一個下方側邊的棱處相交面是四邊形、五邊形、六邊形。對正六邊形而言,棱處相交面皆為四邊形、五邊形、六邊形。
- 頂點處相交面與頂點處相交棱
- 頂點處相交面為6個多邊形,包含兩個梯形、三個五邊形以及一個六邊形。頂點處相交棱則有4條。
參見
[编辑]註釋
[编辑]參考文獻
[编辑]- ^ What Are Polyhedra?, with Greek Numerical Prefixes
- ^ proof of platonic solids (页面存档备份,存于互联网档案馆) mathsisfun.com [2016-1-10]
- ^ Self Dual Tridecahedron (页面存档备份,存于互联网档案馆) dmccooey.com [2016-1-10]
- ^ Counting polyhedra (页面存档备份,存于互联网档案馆) numericana.com [2016-1-10]
- ^ Wolfram, Stephen. "Hendecagon prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ 6.0 6.1 Wolfram, Stephen. "Dodecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Weisstein, Eric W. (编). Biaugmented Pentagonal Prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Oblate Rhombohedra (页面存档备份,存于互联网档案馆) science.unitn.it [2016-1-10]
- ^ Virtual Polyhedra, Greek Numerical Prefixes (页面存档备份,存于互联网档案馆), 1996, George W. Hart, georgehart.com [2016-1-10]
- ^ 10.0 10.1 A space-filling polyhedron with 13 faces (页面存档备份,存于互联网档案馆) science.unitn.it [2016-1-10]











