錐台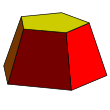  例如:五角錐台與四角錐台 |
| 類別 | 錐台 |
|---|
| 對偶多面體 | 不對稱雙錐體 |
|---|
| 性質 |
|---|
| 面 |  |
|---|
| 邊 |  |
|---|
| 頂點 |  |
|---|
| 歐拉特徵數 | F= , E= , E= , V= , V= (χ=2) (χ=2) |
|---|
| 組成與佈局 |
|---|
| 面的種類 | n 个梯形, 2 个n边形 |
|---|
| 對稱性 |
|---|
| 對稱群 | Cnv, [1,n], (*nn) |
|---|
| 特性 |
|---|
| 凸多面体 |
| 圖像 |
|---|
|
|
註: 為底面邊數 。 為底面邊數 。 |
|
棱台是几何学中研究的一类多面体,指一个棱锥被平行于它的底面的一个平面所截後,截面与底面之间的几何形体。截面也称为棱台的上底面,原来棱锥的底面称为下底面。随着棱锥形状不同,棱台的称呼也不相同,依底面多边形而定,例如底面是正方形的棱台称为方棱台,底面为三角形的棱台称为三棱台,底面为五边形的棱台称为五棱台等等。棱台是平截头体的一类,也是更广义的拟柱体的一种。根据所截的是圆锥还是棱锥,可分为圆台与棱台。
从棱台的定义可以推知,一个以n边形为底面的棱台,一共有2n个顶点,n+2个面以及3n条边。棱台的对偶多面体是双锥。棱台的对称性取决于原来棱锥。如果原来的棱锥是正棱锥,那么棱台和正多边形有相同的对称结构(同构的对称群)。
棱台的体积取决于两底面之间的距离(棱台的高),以及原来棱锥的体积。设 為棱台的高,
為棱台的高, 和
和 為棱台的上下底面積,
為棱台的上下底面積, 為棱台的体积。由于棱台是由一个平面截去棱锥的一部分(也就是和原来棱锥相似的一个小棱锥)得到,所以计算体积的时候,可以先算出原来棱锥的体积,再减去和它相似的小棱锥的体积。棱锥被平行于底面的平面所截时,截面的面积与底面面积的比,等于小棱锥和原棱锥的高的比的平方。假设原棱锥的高是
為棱台的体积。由于棱台是由一个平面截去棱锥的一部分(也就是和原来棱锥相似的一个小棱锥)得到,所以计算体积的时候,可以先算出原来棱锥的体积,再减去和它相似的小棱锥的体积。棱锥被平行于底面的平面所截时,截面的面积与底面面积的比,等于小棱锥和原棱锥的高的比的平方。假设原棱锥的高是 ,那么小棱锥的高是
,那么小棱锥的高是 。也就是说:
。也就是说:

所以:

棱台的体积等于原棱锥体积减去小棱锥的体积:

对于正棱锥,假设它的底面是正n边形,边长分别为a和b,高是h,那么底面积是: 所以它的体积是:
所以它的体积是:

棱台的侧面展开图是由各个梯形侧面组成的,展开图的面积,就是各个侧面的面积之和,也就是原棱锥的侧面积减去小棱锥的侧面积Sc
 ,其中
,其中 是第 i 个侧面的面积。
是第 i 个侧面的面积。
棱台的表面积等于棱台的侧面积Sc加上底面积S。假设各个梯形侧面的高是hi,底边的长度是ai和bi,那么棱锥的侧面积:

棱台或圆台的体积是原立体图形的体积减去被截去部分的体积:

B1 指一个底面的面积,B2指另一个底面的面积, and h1, h2 指原顶点分别到两底面的面积。
考虑到

这个体积也可用平截头体的高 h = h2−h1 与两底面面积的希罗平均数表达:

亚历山大里亚的希罗 推导出了这个公式并且凭借它遇到了虚数。[1]
特别地, 圆台的体积是

π 等于 3.14159265...,'R1, R2 是两底面的半径。
 Pyramidal frustum.
Pyramidal frustum.
底面为n边形的棱台的体积是

a1 与 a2 是底面的边长。
对于一个正圆台,[2]

![{\displaystyle {\begin{aligned}{\text{Total Surface Area}}&=\pi \left[(R_{1}+R_{2})s+R_{1}^{2}+R_{2}^{2}\right]\\&=\pi \left[(R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}+R_{1}^{2}+R_{2}^{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b8201057855f7fa983fa2497704c9519c068b24)
Lateral Surface Area指侧面积,Total Surface Area指总面积,R1 and R2 为底面半径,s 为平截头体的斜高。
一个底面为正n边形的正棱台的表面积是
![{\displaystyle A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe2ca30c9417908ab3b1e7cacd952dd58ac0283)
a1 与 a2是两底面的边长。
- 金字塔:某些金字塔是棱台状建筑,大部分是四棱台;
- 圓台:平行于圆锥底面的平面截圆锥,截面和底面之间的部分;
- 棱锥:多边形的各个顶点与平面外一点相连得到的几何体。
- 雙錐台
- 錐體
- ^ Nahin, Paul. "An Imaginary Tale: The story of the square root of minus one." Princeton University Press. 1998
- ^ Mathwords.com: Frustum. [17 July 2011]. (原始内容存档于2021-01-26).































![{\displaystyle {\begin{aligned}{\text{Total Surface Area}}&=\pi \left[(R_{1}+R_{2})s+R_{1}^{2}+R_{2}^{2}\right]\\&=\pi \left[(R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}+R_{1}^{2}+R_{2}^{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b8201057855f7fa983fa2497704c9519c068b24)
![{\displaystyle A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe2ca30c9417908ab3b1e7cacd952dd58ac0283)