正多面體
| 部分的正多面體 | |
|---|---|
 正八面體 (柏拉圖立體) |
 大十二面體 (克卜勒-龐索立體) |
 星形八面體 |
 四角六片四角孔扭歪無限面體 |
在幾何學中,正多面體是同時具有等邊、等角和等面特性的多面體。在經典語境中,有許多描述上不同但實際上等價的定義存在,最常見的定義是每個面都是全等的正多邊形,且每個頂點都是相同數量且相同種類之正多邊形的公共頂點。例如立方體是一種正多面體,其每個面都是正方形,且每個頂點都是3個正方形的公共頂點。在中文環境中,一般被大眾認知的正多面體通常代表只有五種的凸正多面體,又稱為柏拉圖立體,其包括了正四面體、立方體、正八面體、正十二面體和正二十面體。然而在定義上,正多面體僅指每個面是正多邊形、每條邊等長每個角等角且每面全等的多面體,而符合上述定義的多面體不一定是凸多面體,也可能是星形多面體、抽象多面體或扭歪多面體等。這些多面體除了五種凸正多面體外,還有四種非凸正多面體(克卜勒-龐索立體)、五種抽象正多面體和五種複合正多面體。
概述[编辑]

在幾何學中,正多面體是一類對稱性可以在其各維度元素的集合(或稱標記[註 1])上傳遞的多面體。正多面體通常具有高度對稱性,其同時具有邊可遞,點可遞和面可遞的性質[註 2],換句話說,即正多面體是同時具有等邊、等角和等面特性的多面體。在經典語境中,有許多描述上不同但實際上等價的定義存在,最常見的定義是每個面都是全等的正多邊形,且每個頂點都是相同數量且相同種類之正多邊形的公共頂點。例如立方體是一種正多面體,其每個面都是正方形,且每個頂點都是3個正方形的公共頂點。
所有正多面體皆可以使用施萊夫利符號來表示,其可以計為{n, m}。其中n表示構成面的頂點數,m則表示與頂點相鄰的多邊形數量。在中文語境中,一般被大眾認知的正多面體通常代表只有五種的凸正多面體,又稱為柏拉圖立體,其包括了正四面體、立方體、正八面體、正十二面體和正二十面體。然而在定義上,正多面體僅指每個面是正多邊形、每條邊等長每個角等角且每面全等的多面體,而符合上述定義的多面體不一定是凸多面體,也可能是星形多面體、抽象多面體或扭歪多面體等。這些多面體除了五種凸正多面體外,還有四種非凸正多面體(克普勒–龐索立體)、五種抽象正多面體和五種複合正多面體。
正多面體[编辑]
一般常見的正多面體為五種正凸多面體,又稱為柏拉圖立體。除了這種凸多面體外,亦有非凸的正多面體,為四種星形正多面體,又稱為克普勒–龐索立體;以及五種正多面體的複合體。
柏拉圖立體[编辑]
廣泛地出現在文化中的五種正多面體。[2]

|

|

|

|

|
| 正四面體 {3, 3} | 立方體 {4, 3} | 正八面體 {3, 4} | 正十二面體 {5, 3} | 正二十面體 {3, 5} |
| χ = 2 | χ = 2 | χ = 2 | χ = 2 | χ = 2 |
克普勒–龐索立體[编辑]
克卜勒-龐索立體的面同樣由正多邊形組成,但其面或邊有自我相交的情形,即非凸多面體。由於外觀如同星狀,因此又稱為星形正多面體。[3]

|

|

|

|
| 小星形十二面體 {5/2, 5} |
大十二面體 {5, 5/2} |
大星形十二面體 {5/2, 3} |
大二十面體 {3, 5/2} |
| χ = −6 | χ = −6 | χ = 2 | χ = 2 |
複合正多面體[编辑]
由多個同一種正多面體組合而成且具有高度對稱性的結構也可以視為正多面體的一種。[4]例如兩個正四面體組成的星形八面體,其類似於由兩個正三角形組成的大衛之星在三維空間中的類比。多個正多面體的複合結構也可以有其他種類,然而其未必會符合標記[註 1]可遞[註 2]的特性,因此不能算是正多面體,例如三複合正八面體。

|

|

|

|

|
| 二複合正四面體 星形八面體 2 {3, 3} |
五複合正四面體 5 {3, 3} |
十複合正四面體 10 {3, 3} |
五複合立方體 5 {4, 3} |
五複合正八面體 5 {3, 4} |
| χ = 4 | χ = 10 | χ = 0 | χ = −10 | χ = 10 |
性質[编辑]
正多面體最基本的特性就是每個面都是全等的正多邊形、每條邊等長且每角等角。
等價性質[编辑]
在定義中,每個頂點周圍有相似的面排佈的性質可以替換成下列的等價條件:
同心球[编辑]
正多面體具有三個相關的球體(其他非正多面體至少缺少一種),其球心位於同一個點上:
廣義的正多面體[编辑]
20世紀出現了一系列關於正多面體概念的概括,導致了正多面體出現了幾個新的種類。
正扭歪無限面體[编辑]
在20世紀最初的幾十年,考克斯特和皮特里考慮了頂點的排佈以及角呈現馬鞍形樣式的多面體類型,並找到了三種由正多邊形組成且無限延伸的折疊形幾何結構,被命名為正扭歪無限面體。[6]
| 三維空間中的正扭歪無限面體的局部 | ||
|---|---|---|
 四角六片四角孔扭歪無限面體 {4,6|4} |
 六角四片四角孔扭歪無限面體 {6,4|4} |
 六角六片三角孔扭歪無限面體 {6,6|3} |
正扭歪多面體[编辑]
如同扭歪多邊形的定義(不共面的多邊形),有限面數的扭歪多面體則為其無法所有面或頂點皆位於同一個三維空間的多面體,因此會需要四維或以上的空間來構造限面數的扭歪多面體,就如同皮特里多邊形為正多面體上的一個不共面封閉路徑,有限面數的扭歪多面體可以從四維正多胞體中取一個不共三維空間的封閉區域來構造。[7]
| 平行考克斯特平面投影 | 球極平面投影 | |||
|---|---|---|---|---|
| A4 | F4 | |||

|

|

|

|

|
| 四角六片三角孔扭歪正三十面體 {4, 6 | 3} |
{6, 4 | 3} | {4, 8 | 3} | {8, 4 | 3} | {4, 4 | n} |
| 30個正方形面 60條邊 20個頂點 |
20個正六邊形面 60條邊 30個頂點 |
288個正方形面 576條邊 144個頂點 |
144個正八邊形面 576條邊 288個頂點 |
n2個正方形面 2n2條邊 n2個頂點 |
位於非歐空間或其他空間的正多面體[编辑]
在非歐幾里德空間(雙曲空間、橢圓空間等)以及諸如複數空間或四元數空間等其他空間被發現之後,對於這些空間幾何學的研究導致了更多新種類的正多面體被發現,如複正多面體[8]等,但這些正多面體只能在特定空間中維持其正的特性。
複數空間的正多面體[编辑]
在幾何中,複數空間的多面體是實數空間中的多面體在複數空間的推廣。[8]
| 名稱 | 黑塞二十七面體 | 雙黑塞二十七面體 | 截半黑塞二十七面體 |
|---|---|---|---|
| 施萊夫利符號 | 3{3}3{3}3 | 2{4}3{3}3 | 3{3}3{4}2 |
| (頂點v、邊e、面f) | (27, 72, 27) | (54, 216, 72) | (72, 216, 54) |
| 面 | 27個3{3}3 |
72個2{4}3 
|
54個3{3}3 |
| 圖像 藍色表示其中一面 |

|

|

|
四元數空間的正多面體[编辑]
在幾何中,四元數空間的多面體是實數空間中的多面體在四元數空間的推廣。其與複數空間類似,點不具有序性,因此沒有「位於...之間」的相互關係,因此一個四元數空間多面體可以被理解為一組點、線和面等的排佈關係,其中,點為多條線的連接點、線連接了多個面。由於四元數的乘法不具有交換率,因此必須透過純量與向量相乘來構建乘法系統,通常會使用左乘法。[10]
四元數空間的正多面體與實數空間的正多面體和複數空間的正多面體一樣,其對稱性皆可以被描述為反射群。例如,一個正的四元數空間直線可以與U1(H)的有限子群一一對應:二元循環群、二元二面體群(參閱一般四元数群章節二元二面體群) 二元四面體群、二元八面體群和二元二十面體群。[11]
雙曲空間的正多面體[编辑]

在H3的雙曲仿緊空間中的正堆砌體或蜂巢結構體通常具有正鑲嵌圖的胞或頂點圖。在這樣的結構中,這些鑲嵌圖可以視為存在角虧並在封閉於一個無窮遠點。若當雙曲正堆砌體或蜂巢結構體位於非緊空間時則其會封閉於2個或以上個無窮遠點甚至是發散。
实射影平面的正多面體[编辑]
另一組正多面體為实射影平面的鑲嵌結構,其包括了立方體半形、八面體半形、十二面體半形和二十面體半形。[12]其皆為(全域)投影多面體,並且對應到四個柏拉圖立體的投影結構。由於正四面體不像其他四個柏拉圖立體一樣擁有相對面,因此正四面體無法形成多面體半形。
 立方體半形 {4,3} |
 八面體半形 {3,4} |
 十二面體半形 {3,5} |
 二十面體半形 {5,3} |
抽象正多面體[编辑]
到目前為止,多面體皆被認為是任意維度之多胞形在三維空間的例子。在20世紀下半葉出現了抽象代數概念的發展,如多面體組合學,最終形成抽像多胞形作為元素偏序关系的概念。抽像多面體的元素包括了它的主體(最大元素)、面、邊、頂點和空多胞形。這些抽像元素可以映射到普通空間或具體化成一個幾何形狀。一些抽象多面體具有良好具像化實例,但不一定所有的抽象多面體都能找到對應的具像化實例。抽象多面體與一般的多面體同樣可以定義標記[註 1]。若一抽象多面體的組合對稱性可以在其標記上傳遞[註 2],則這個抽象多面體為抽象正多面體,換句話說,即任何標記都可以在多面體的對稱性下映射到任何其他標記上。
在考克斯特於1977年出版的著作《正多胞形》中列出了五種不存在良好具像化實例的抽象正多面體。後來在1987年耶爾格·邁克爾·威利的論文又再次的確定了共存在五種有這種性質的抽象正多面體。[13]這五種抽象多面體都具有C2×S5對稱性,但只能具像化出一半的對稱性,即C2×A5或二十面體群對稱性。[14][15][16]
| 多面體 |  內側菱形三十面體 |
 截半大十二面體 |
 內側三角六邊形二十面體 |
 雙三斜十二面體 |
 凹五角錐十二面體 |
|---|---|---|---|---|---|
| 種類 | {4,5}6 | {5,4}6 | {6,5}4 | {5,6}4 | {6,6}6 |
| 頂點圖 | {5}, {5/2} |
(5.5/2)2
|
{5}, {5/2} |
(5.5/3)3
|

|
| 面 | 30個菱形 |
12個五邊形 12個五角星 |
20個六邊形
|
12個五邊形 12個五角星 |
20個六邊形
|
| 鑲嵌 |  {4, 5} |
 {5, 4} |
 {6, 5} |
 {5, 6} |
 {6, 6} |
| χ | −6 | −6 | −16 | −16 | −20 |
皮特里對偶[编辑]
柏拉圖立體的皮特里對偶是一種正則地區圖,其頂點和邊對應於原始多面體的頂點和邊,其面是扭歪皮特里多邊形的集合。[17]
| 名稱 | 皮特里正四面體 | 皮特里立方體 | 皮特里正八面體 | 皮特里正十二面體 | 皮特里正二十面體 |
|---|---|---|---|---|---|
| 施萊夫利符號 | {3,3}π、 {4,3}3 | {4,3}π、 {6,3}4 | {3,4}π、 {6,4}3 | {5,3}π、 {10,3} | {3,5}π、 {10,5} |
| (頂點數,邊數,面數), χ | (4,6,3), χ = 1 | (8,12,4), χ = 0 | (6,12,4), χ = −2 | (20,30,6), χ = −4 | (12,30,6), χ = −12 |
| 面 | 3個正扭歪四邊形
|
4個正扭歪六邊形 | 6個正扭歪十邊形 | ||

|

|

|

| ||
| 圖像 | 
|

|

|

|

|
| 旋轉動畫 | 
|

|

|

|

|
| 相關圖 |  {4,3}3 = {4,3}/2 = {4,3}(2,0) |
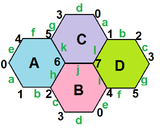 {6,3}3 = {6,3}(2,0) |
 {6,4}3 = {6,4}(4,0) |
 {10,3}5 |
{10,5}3 |
球面多面體[编辑]
五個凸正多面體和四個星形多面體皆可以表示成球面多面體,或球面鑲嵌:
 正四面體 {3,3} |
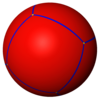 立方體 {4,3} |
 正八面體 {3,4} |
 正十二面體 {5,3} |
 正二十面體 {3,5} |
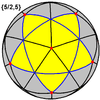 小星形十二面體 {5/2,5} |
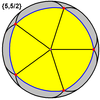 大十二面體 {5,5/2} |
 大星形十二面體 {5/2,3} |
 大二十面體 {3,5/2} |
只能存於球面的正多面體[编辑]
 二角形二面體 {2,2} |
 正三角形二面體 {3,2} |
 正方形二面體 {4,2} |
 正五邊形二面體 {5,2} |
 正六邊形二面體 {6,2} |
... | {n,2} |
 正二面形 {2,2} |
 正三面形 {2,3} |
 正四面形 {2,4} |
 正五面形 {2,5} |
 正六面形 {2,6} |
... | {2,n} |
相關多面體[编辑]
部分多面體雖然不是正多面體,但與正多面體有一定的關連。
正多邊形多面體[编辑]
| 部分的正多邊形多面體 | |
|---|---|
 正十二面體 |
 小斜方截半立方体 |
 雙新月雙罩帳 |
 五角星柱 |
正多邊形多面體或稱正多邊形面多面體(Regular-faced Polyhedron)是指所有面都是正多邊形的多面體。[18]在三維空間中,所有面都是正多邊形不一定能滿足正多面體的定義,例如92種詹森多面體雖然所有面都是正多邊形但都不是正多面體。正多邊形多面體可以分為以下幾類:[19]
| 凸多面體 | 等面 | 等角 | 種類 | 數量 |
|---|---|---|---|---|
| 是 | 是 | 是 | 凸正多面體(柏拉圖立體) | 5 |
| 是 | 是 | 否 | 凸正三角面多面體(正四面體、正八面體、正二十面體除外,因為此三者為柏拉圖立體,是等角圖形) | 5(凸正三角面多面體有8個[20],但是扣掉3個) |
| 是 | 否 | 是 | 正角柱、正反角柱 | ∞ |
| 阿基米德立體 | 13 | |||
| 是 | 否 | 否 | 詹森多面體(J12、J13、J17、J51、J84除外,因為此五者為三角面多面體,所有面全等) | 87(詹森多面體有92個,但是扣掉5個) |
| 否 | 是 | 是 | 星形正多面體(克卜勒-龐索立體) | 4 |
| 否 | 是 | 否 | 非凸正三角面多面體(含多連正四面體)、多連立方體(正方形面不共面的情況)、多連正十二面體 | ∞ |
| 否 | 否 | 是 | 正星形柱、正星形反柱(皆屬於柱狀均勻多面體) | ∞ |
| 星形均勻多面體 | 53[21] | |||
| 否 | 否 | 否 | 其他由正多邊形組成的非凸多面體(例如側錐七角柱) | ∞ |
有n個面的凸正多邊形多面體的個數為(從n=1開始):
- 0、0、0、1、2、3、2、7、3、6、4、7、3、13、2、5、4、6、1、9、2、6、1、4、1、8、4、2、1、3、1、10、1、3、1、2、4、3、1、2、1、9、1、2、1、2、2、2、1、2、1、9、1、2、1、2、1、2、1、2、1、9、1、2、... (OEIS數列A180916)
有n個頂點的凸正多邊形多面體的個數為(從n=1開始):
- 0、0、0、1、2、3、3、6、5、7、4、10、1、6、5、6、0、6、0、8、1、4、1、8、4、2、0、3、0、9、0、3、0、2、3、2、0、2、0、5、0、2、0、2、1、2、0、3、0、5、0、2、0、2、4、2、0、2、0、10、0、2、0、2、1、2、... (OEIS數列A333660)
稀有多面體[编辑]
| 部分的稀有多面體 | |
|---|---|
 正十二面體 |
 冠狀多面體 |
 小星形十二面體 |
![D-星形二十面體[22][23]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Stellation_icosahedron_d.png/120px-Stellation_icosahedron_d.png) D-星形二十面體[22][23] |
稀有多面體是指同時具備面可遞和點可遞的立體,也就是說這類立體既是等面的也是等角的,由於三維空間的複雜性,要滿足此特性並不容易,因此稱稀有多面體。稀有多面體不一定是正多面體,因為稀有多面體不一定滿足等邊(邊可遞)的特性,但所有正多面體都是稀有多面體。
參見[编辑]
註解[编辑]
- ^ 1.0 1.1 1.2 多面體標記是一系列多面體元素的集合,這個集合中會包括1個多面體的主體、多面體的其中一個面、前者提到的面中的其中一條稜、前者提到的稜中的其中一個頂點和一個空多胞形。
- ^ 2.0 2.1 2.2 在多面體中,某種元素的「可遞」性質代表這立體上的任意兩個同類元素A和B,透過在該立體的對稱性下旋轉或鏡射這個立體,使A移動到B原來的位置時,其元素仍然佔據了相同的空間區域[1]。
參考文獻[编辑]
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at mpiz-koeln.mpg.de
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- ^ McLean, K. Robin, Dungeons, dragons, and dice, The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822.
- ^ 欧几里得. 燕晓东 , 编. 几何原本. 北京: 人民日报出版社. 2005年5月. ISBN 7-80208-294-3.
- ^ Coxeter, Star polytopes and the Schläfli function f(α,β,γ) p. 121 1. The Kepler–Poinsot polyhedra
- ^ Coxeter, Harold Scott MacDonald. Regular Polytopes Third. Dover Publications. 1973: 48 [1948] [2019-09-13]. ISBN 0-486-61480-8. OCLC 798003. (原始内容存档于2016-05-10).
- ^ Cromwell, Peter R. Polyhedra. Cambridge University Press. 1997: 77. ISBN 0-521-66405-5.
- ^ Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
- ^ Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.
- ^ 8.0 8.1 Coxeter, Complex Regular polytopes,[9] Table V. The nonstarry regular polyhedra and 4-polytopes. p. 180.
- ^ Coxeter, H.S.M., Regular Complex Polytopes, Cambridge University Press, 1991, ISBN 0-521-39490-2
- ^ Davis, C.; Grünbaum, B.; Sherk, F.A. The Geometric Vein: The Coxeter Festschrift - Google Books. 2012-12-06 [2016-04-15]. ISBN 9781461256489.
- ^ Hans Cuypers. Regular quaternionic polytopes. Linear Algebra and Its Applications. September 1995,. 226-228: 311–329. doi:10.1016/0024-3795(95)00149-L.
- ^ Coxeter, Introduction to geometry, 1969, Second edition, sec 21.3 Regular maps, p. 386-388
- ^ Wills, Jörg Michael. The combinatorially regular polyhedra of index 2. aequationes mathematicae (Springer). 1987, 34 (2-3): 206––220.
- ^ David A. Richter. The Regular Polyhedra (of index two). 西密西根大學. (原始内容存档于2016-03-04).
- ^ Regular Polyhedra of Index Two, I (页面存档备份,存于互联网档案馆) Anthony M. Cutler, Egon Schulte, 2010
- ^ Regular Polyhedra of Index Two, II (页面存档备份,存于互联网档案馆) Beitrage zur Algebra und Geometrie 52(2):357–387 · November 2010, Table 3, p.27
- ^ McMullen, Peter; Schulte, Egon, Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications 92, Cambridge University Press: 192, 2002, ISBN 9780521814966
- ^ Robert R Tupelo-Schneck. Regular-faced Polyhedra. [2023-01-31]. (原始内容存档于2022-11-14).
- ^ Tom Gettys. Polyhedral Solids. comcast.net. [2022-07-17]. (原始内容存档于2014-04-18).
- ^ Freudenthal, H; van der Waerden, B. L., Over een bewering van Euclides ("On an Assertion of Euclid"), Simon Stevin, 1947, 25: 115–128 (荷兰语)(其表明只有8個凸正三角面多面體)
- ^ Introducing the Kasparian Solids. quantimegroup.com. [2019-09-27]. (原始内容存档于2018-08-31).
- ^ Klitzing, Richard. noble {9,3} modwrap within srid. bendwavy.org. [2021-10-15].
- ^ George W. Hart. Polyhedra with Equal Faces and Equal Vertex Figures. Virtual Polyhedra, georgehart.com. 1996 [2021-10-15]. (原始内容存档于2020-02-24).
外部連結[编辑]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
