球面
| 几何学 |
|---|
 |
| 几何学家 |
|
|
球面 (英語:sphere)是三维空间中完全圆形的几何物体,它是圆球的表面(类似于在二维空间中,“圆 ”包围着“圆盘”那样)。
就像在二维空间中的圆的定义一样,球面在数学上定义为三维空间中离给定的点距离相同的点的集合 r。 [1] 这个距离 r 是球的半径 ,球(ball)则是由离给定点距离小于 r 的所有点构成的几何体,而这个给定点就是球心。球的半径和球心也是球面的半径和中心。两端都在球面上的最长线段通过球心,其长度是其半径的两倍;它是球面和球体的直径 。
尽管在数学之外,术语“球面”和“球”有时可互换使用,但在数学中是明确区分的:球面是一种嵌在三维欧几里得空间内的二维封闭曲面,而球是一种三维图形,其包括球面和球面内部的一切(闭球),不过更常见的定义是只包括球面内部的所有点,不包括球面上的点(开球)。这种区别并不总是保持不变,尤其是在旧的数学文献里,sphere(球面)被当作固体。这与在平面上混用术语“圆”(circle)和“圆盘”(disk)的情况类似。
三维空间中的方程[编辑]
在解析几何中,球心为 (x0, y0, z0),半径为 r 的球面是满足下面方程的所有点 (x, y, z) 的轨迹
令 a, b, c, d, e 为实数,a ≠ 0,并且
如果 ,则那么下面的方程
没有实数根,称为虚球面的方程。如果 ,则 的唯一解是点 ,此时该方程称作点球面的方程。还有一种,就是在 的情况下, 是球面的方程,其中心是,半径是。[1]
如果上述等式中的 a 是零,那么 f(x, y, z) = 0 就成为了平面方程。因此,平面可以认为是球心在无穷远点的球面。[2]
半径 ,中心在 的球面上的点可以写成参数方程
以原点为中心的任意半径的球面是以下微分形式的积分曲面:
这个方程反映了在球面上行进的点的位置 (x, y, z) 和速度向量 (dx, dy, dz) 总是彼此正交的。
球面还可以通过以任何直径为轴,把圆旋转一周形成的表面来构造。由于圆是一种特殊的椭圆 ,所以球面也是一种特殊的椭球面。椭圆围绕其长轴旋转形成的曲面,就是长球面;如果绕短轴旋转,就会形成一个扁球面。[4]
包围的体积[编辑]
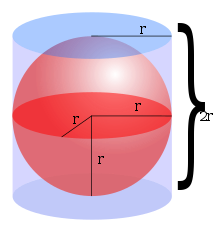
其中 r 是球面的半径。阿基米德首先推导出了这个公式,他通过证明球体内的体积是球体内部与外接圆柱体(具有与球体直径相等的高度和直径)内部之间的体积差值的两倍而得出该公式。[5] 这个说法可以根据祖暅原理得到。该公式也可以使用积分得出,即用截面积分(定积分)对无穷多的厚度无穷小的圆盘沿 x 轴从 x = −r 到 x = r 堆积起来的体积求和,假设该球面半径为 r,以原点为球心。
在任何给定的 x 处,体积增量(ΔV)近似等于 x 处圆盘的面积与其厚度(Δx)的乘积:
当最厚的那一个圆盘厚度趋近0时,总体积是所有增量的总和:
其中 ||T || 表示当取分割 T 时,最厚的那个圆盘的厚度。此时体积为:
在任何给定的 x 处,x、y、r 都可以构成一个直角三角形;因此,应用勾股定理得出:
将上式代入得到
积分之后就可以得出结果
另外,此公式也可以用球坐标系计算,体积元可以写成
因此得到三重积分,并算出结果如下:
对于大多数实际用途而言,立方体的内接球的体积可以近似为立方体体积的52.4%,这是因为 V = π/6 d3,其中 d 是球面的直径,也是立方体的边长,π/6 ≈ 0.5236。例如,直径1m的球的体积是边长为1m的立方体体积的52.4%,或约0.524 m3。
表面积[编辑]
半径为r的球体的表面積为:
阿基米德首先根据“外接圆柱体侧面的投影是保持面积的”这个事实推导出这个公式[6]。[7] 另一种得到这个公式的方法基于如下事实,即球的表面积等于其体积公式关于 r 的导数 ,因为半径为 r 的球体的体积可以认为是从半径0到半径 r 嵌套在一起的无穷小厚度的无穷多个同心球壳的表面积的总和。在无穷小的厚度下,任何给定球壳的内外表面面积是相等的,半径 r 处的体积元可以简单地认为是半径 r 处的表面积与无穷小厚度的乘积。
在任何给定半径 r 处,[8] 体积增量(ΔV)等于半径 r 处表面积(A(r))与球壳厚度(Δr)的乘积:
总体积是所有球壳体积的总和:
该等式在最厚的那一个圆盘的 Δr 趋近于 0 时[9]为:
代入 V:
将等式两边对 r 求导就会得到 A 关于 r 的函数:
这通常写为:
其中 r 是球面的半径。
再来看一种方法,球面上的面积元可以用球坐标系给出:dA = r2 sin φ dθ dφ。用笛卡尔坐标来表示的话,面积元就会写成
更一般性的表达,请参阅面积元条目。
因此总面积可以通过积分得到:

球面是包围给定体积的所有曲面中面积最小的,球面还是给定表面积的所有闭合曲面中包围体积最大的。因此球面在自然界中出现:例如,气泡和小水滴大致为球形,因为表面张力会局部最小化表面积。
球的质量与表面积之比称为比表面积,可以由上述等式表示出来
其中 ρ 为密度(质量与体积之比)。
几何性质[编辑]
球面由四个不共面的点唯一确定。更一般地说,球面由四个条件唯一确定,例如通过一个点、与一个平面相切,等等。 [11] 该性质类似于三个非共线的点确定平面中的唯一圆的性质。
因此,一个球体由一个圆和一个不在该圆平面内的点唯一确定。
通过检查两个球面方程的共同解,可以看出两个球相交于一个圆,包含该圆的平面称作相交球的基本平面 。[12] 虽然基本平面是一个实平面,但这个圆可能是虚圆(两个球面没有实的公共点),也可能由单个点组成(两个球面在该点相切)。[13]
在实交点处的两个球面之间的夹角是由该点处的球体的切面确定的二面角。两个球面在相交圆的所有点处的夹角都是相同的。[14] 当且仅当它们的球心之间的距离的平方等于其半径的平方和时,它们的交角才是直角(相互正交)。[2]
球面束[编辑]
如果 f(x, y, z) = 0 和 g(x, y, z) = 0 是两个不同球面的方程,那么
当参数 s 和 t 是任意值时,也是球面方程。满足该等式的所有球体的集合称为由原始两个球体确定的球面束。在这个定义中,允许球面是一个平面(无限半径,球心在无穷远处),而如果两个原始球面都是平面,那么束的所有球面都是平面,否则在球面束中只会有一个平面(基本平面)。[2]
如果球面束不是由所有平面组成,那么有三种类型的束:[13]
- 若球面相交于一个实圆 C,则球面束由包含 C 的所有球面(包括基本平面)组成。球面束中所有普通球面的中心位于穿过 C 的中心并垂直于基本平面的直线(下面称作“中心线”)上。
- 若球面相交于一个虚圆,球面束的所有球面也会通过这个虚圆,但是其实这些普通球面不相交(没有真正的公共点)。中心线垂直于这个基本平面,这是一个真实的平面,但其中包含了一个假想的圆。
- 如果球面相交于一点 A,则所有在这个面内的球面 A 都是相切的,同时基本面是所有这些面的公切面。中心线在 A 处垂直于基本平面。
所有从基本平面的固定点到球面束的一个球面的切线的长度都是相同的。 [13]
基本平面是与球面束中所有球面正交的所有球面的中心的轨迹。而且,与球体束的任何两个球体正交的球体,与球面束的所有球面正交,并且其中心位于球面束的基本平面中。 [13]
术语[编辑]
穿过球心的一条直线与球面相交,这两个相对称的交点称为对径点。大圆是球面上的一个圆,与球面具有相同的中心和半径,大圆所在的平面能将球面分成两个相同的部分。球面的截面称为圆面截口(spheric sections)。圆面截口均为圆,除了大圆以外的其他圆称为小圆。 [15]
球面上两个不同非对径点之间的最短距离是过这两个点的唯一大圆上的两个圆弧中劣弧的长度。有了这个“大圆距离”,大圆就成为了黎曼圆。
若将球面上任意一点设为该球面的北极,与该点相对应的对径点则被称为南极,而赤道则是与这两个极点等距的大圆。 过这两个极点的大圆被称为子午线或经线,过这两个极点的直线被称为旋转轴。而纬度则是球面上与赤道平行的圆。这个术语也同样适用于那些与地球表面一样近似于球面的天体 (见大地水准面)。
半球面[编辑]
任何过球心的平面都把它分成两个相等的半球面。过球心的任何两个相交平面都将球体细分为四个球面二角形,其顶点全部与位于平面交线上的对径点重合。
球体的对径商空间是实射影平面,它也可以被看作是北半球,赤道的对映点被确定。
有猜想认为半球是黎曼圆的最佳(最小面积)等长填充。
推广[编辑]
维数[编辑]
球面可以推广到任意维数的空间。对于任意自然数n,n-球面(常写为Sn)是(n + 1)维欧几里得空间中离该空间的一个中心点距离固定为r的点的集合,其中r与前面一样是正实数。特别地:
n > 2的球面有时称作超球面 。
以原点为中心的单位半径n球面表示为Sn,通常称为“n球面”。请注意,普通球面是一个2-球面,因为它是一个二维曲面(它嵌入在三维空间中)。
单位(n-1)-球面的表面积是
其中Γ(z)是欧拉发现的伽马函数 。
表面积的另一种表达式为
体积等于表面积乘以r/n,或者说
对于n球的体积也存在一般递归公式。
度量空间[编辑]
更一般地,在度量空间 (E,d) 中,中心x、半径r > 0的球面是使得d(x,y) = r的点y的集合。
如果球心是位于E的原点(如在赋范空间中那样)的话,定义和符号中没有提及它。如果等于1,则半径也是如此,例如单位球体的情况。
与球体不同的是,即使是一个大球面也可能是一个空集。例如,在欧几里德度量 Zn 中,只有r2可以写成整数的n平方和时,半径r的球面才是非空的。
拓扑学[编辑]
在拓扑学中,n球面定义为与(n + 1)球体的边界同胚的空间;因此它与欧几里德n球体同胚 ,但可能缺少其度量 。
n球面记为Sn 。它是没有边界的紧致拓扑流形的一个例子。球面不必是光滑的;如果它是光滑的,它就不需要与欧几里得球面微分同胚 。
海涅-博雷尔定理表明欧几里德n球面是紧致的。球面是连续函数||x||下单点集的逆象。因此,球面是闭合的。Sn也是有界的;所以它是紧致的。
值得注意的是,在三维空间中是可以把普通的球面内外翻转过来的,这个过程称作球面外翻,过程中可能会发生自交,但不会产生任何折痕。
球面几何[编辑]

欧几里得平面几何的基本要素是点和线。在球面上,点以通常的意义来定义。“线”的类似物是测地线,测地线是一个大圈;大圆的界定性特征是含有其所有点的平面也穿过球心。弧长测量表明,球面上两点之间的最短路径是过这两点的大圆的较短的那一段圆弧。
经典几何的许多定理也适用于球面几何,但并非所有的定理都是这样,因为球面不能满足一些经典几何的假设,包括平行假设。在球面三角学中,角是在大圆之间定义的。球面三角学在许多方面与普通的三角学不同。例如,球形三角形的内角之和总是超过180度。而且,任何两个相似的球面三角形都是全等的。
球面的十一种性质[编辑]

在David Hilbert和Stephan Cohn-Vossen的著作《几何与想象》 [16]一书中,统一描述了球面的11种性质,并讨论了这些性质是否仅仅存在于确定球面之中。一些性质对于平面来说也是成立的,因为平面可以视作半径无限大的球面。这些性质为:
- 球面上任意点与球心的距离都是相同的。同时,它和某两个固定点之间的距离之比是恒定的。
- 第一句一般是球面的定义,可以唯一确定球面。而第二句的结论与阿波罗尼斯圆类似,很容易被推导出,第二句的结论也适用于平面。
- 球面的外轮廓和用平面截出的截面都是圆。
- 该性质是球面独有的性质。
- 球面的径长和周长保持不变。
- 曲面的径长是指两个与该曲面相切的互相平行的平面的距离。除了球面之外,还有很多的闭合凸面的径长也是恒定不变的,例如迈斯纳结构 。而曲面的周长是在平面上的正交投影的边界长度。从这两者中任意性质出发都可以推出另一个性质。
- 球面的所有点都是脐点 。
- 球体是没有中心表面的。
- 球面上的所有测地线都是闭合曲线。
- 测地线是球面表面上的曲线,也是两点之间的最短距离。它们是平面几何中直线概念的一种概括性表达。对于球面来说,测地线是一个大的圆。许多其他的曲面都有这种性质。
- 在体积大小一定的情况下,球面的表面积最小;而在表面积的大小固定的情况下,球面则能包围最大的体积。
- 在所有已经给定表面积的凸固体中,球面的总平均曲率是最小的。
- 平均曲率是两个主曲率的平均值,这是恒定的一个数值,因为球面上的所有点的主曲率都是相等的。
- 球面的平均曲率是恒定的。
- 球面是唯一没有边界和奇异点而有恒定正平均曲率的嵌入面。其他如最小曲面这样的沉浸面的平均曲率也是恒定的。
- 球面的高斯曲率是一个常数。
- 球面是由一个由三参数所组成的刚性运动所构成的。
- 围绕任何轴旋转,在原点处的单位球会将球面阴影映射到其自身上。任何绕着过原点的直线的旋转都可以表示为在三坐标轴上旋转的组合
(详见欧拉角)。因此,存在一个三参数的旋转族,使得每次旋转将球面转换成自身;这个族被称为旋转组SO(3)。该平面是唯一具有三参数变换族的一个曲面(沿原点周围的xy轴旋转和平移)。圆柱体是唯一具有双参数系列刚性运动的表面,并且旋转表面和螺旋面是具有单参数系列的表面。
参见[编辑]

注释[编辑]
- ^ 1.0 1.1 Albert 2016,p. 54
- ^ 2.0 2.1 2.2 Woods 1961,p. 266
- ^ Kreyszig (1972, p. 342)
- ^ Albert 2016,p. 60
- ^ Steinhaus 1969,p. 223
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Steinhaus 1969,p. 221
- ^ r在这个计算中被认为是一个变量
- ^ Pages 141, 149. E. J. Borowski; J. M. Borwein. Collins Dictionary of Mathematics. 1989. ISBN 0-00-434347-6.
- ^ New Scientist | Technology | Roundest objects in the world created 互联网档案馆的存檔,存档日期2015-04-26.
- ^ Albert 2016,p. 55
- ^ Albert 2016,p. 57
- ^ 13.0 13.1 13.2 13.3 Woods 1961,p. 267
- ^ Albert 2016,p. 58
- ^ Weisstein, Eric W. (编). Wolfram MathWorld (首頁). at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Hilbert, David; Cohn-Vossen, Stephan. Geometry and the Imagination 2nd. Chelsea. 1952. ISBN 0-8284-1087-9.
参考文献[编辑]
| 英文维基文库中的《1911年版大英百科全書》條目:Sphere |
- Albert, Abraham Adrian, Solid Analytic Geometry, Dover, 2016 [1949], ISBN 978-0-486-81026-3
- Dunham, William. The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities. : 28, 226. ISBN 0-471-17661-3.
- Kreyszig, Erwin, Advanced Engineering Mathematics 3rd, New York: Wiley, 1972, ISBN 0-471-50728-8
- Steinhaus, H., Mathematical Snapshots Third American, Oxford University Press, 1969
- Woods, Frederick S., Higher Geometry / An Introduction to Advanced Methods in Analytic Geometry, Dover, 1961 [1922]
外部链接[编辑]
| 维基词典上的字词解释 | |
| 维基共享资源上的多媒体资源 | |
| 维基新闻上的新闻 | |
| 维基语录上的名言 | |
| 维基文库上的原始文献 | |
| 维基教科书上的教科书和手册 | |
| 维基学院上的學習资源 | |
| ||||||||||||





















![{\displaystyle V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\right)={\frac {4}{3}}\pi r^{3}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c081de9760153a5ab7e59be1b9de1aa97d08dec)










![{\displaystyle A=\int _{0}^{2\pi }\mathrm {d} \theta \,\int _{0}^{\pi }r^{2}\sin {\varphi }\mathrm {d} \varphi =\int _{0}^{2\pi }[-r^{2}\cos {\varphi }]_{0}^{\pi }\,\mathrm {d} \theta =4\pi r^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4a27c8ea81d50d501df7fb3bb0bff593f198ad3)




