九面體
| 部分的九面體 | |
|---|---|
 三維的關聯多面體 |
 四方半偏方面體 |
 雙三角錐柱 |
 正四角錐柱 |
 七角柱 |
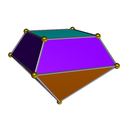 正四角錐柱的對偶 |
在幾何學中,九面體是指由9個面組成的多面體,而邊長全部等長的九面體是七角柱是一種半正多面體。在九面體中,四角錐柱和它的對偶多面體都是九面體。
凸九面體
[编辑]在所有凸九面體中,包含鏡射像共有2606種拓樸結構明顯差異的凸九面體[1][2]。其中有8種具有7個頂點、74種具有8個頂點、296種具有9個頂點、633種具有10個頂點、768種具有11個頂點、558種具有12個頂點、219種具有13個頂點和50種具有14個頂點的凸九面體。這些數據最早紀錄在托馬斯·柯克曼於1870年代出版的書籍中[3]。
常見的九面體
[编辑]七角柱
[编辑]
七角柱是一種底面為七邊形的柱體,是九面體的一種,由9個面21條邊和14個頂點組成[4],對偶多面體為雙七角錐[5]。正七角柱代表每個面都是正多邊形的七角柱,其每個頂點都是2個正方形和1個七邊形的公共頂點,因此具有每個角等角的性質,可以歸類為半正九面體。而頂點都是2個正方形和1個七邊形的公共頂點的這種頂角,在頂點圖中以表示。正七角柱在施萊夫利符號中可以利用{7}×{} 或 t{2, 7}來表示;在考克斯特—迪肯符号中可以利用![]()
![]()
![]()
![]()
![]() 來表示;在威佐夫符號中可以利用2 7 | 2來表示;在康威多面體表示法中可以利用P7來表示。若一個正七角柱底邊的邊長為、高為,則其體積和表面積為[6]:
來表示;在威佐夫符號中可以利用2 7 | 2來表示;在康威多面體表示法中可以利用P7來表示。若一個正七角柱底邊的邊長為、高為,則其體積和表面積為[6]:
八角錐
[编辑]
八角錐是一種底面為八邊形的錐體,是九面體的一種,其由9個面、16條邊和9個頂點組成[7],對偶多面體是自己本身[8]。正八角錐是一種底面為正八邊形的八角錐。若一個正八角錐底邊的邊長為、高為,則其體積和表面積為[8]:
九面體圖
[编辑]
頂點最少且鄰接矩陣有特徵值相等之多重集的兩個圖是一組九面體圖,也就是說最小的等譜多面體圖是一對九面體圖[9],其有八個頂點。
空間充填九面體
[编辑]透過切割菱形十二面體的其中四個面的長對角線可以得到一個自身對偶的九面體,即具有大正方形面、四個菱形面和4個等腰三角形面的四方半偏方面體。如同菱形十二面體,這個九面體同樣可以完全堆滿三維空間[10]。
戈德堡在1982年發現至少有40拓撲不同的空間充填九面體[11]。
九面體列表
[编辑]| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|---|
| 七角柱 | 稜柱體 | 
|
t{2,7} {7}x{} |
14 | 21 | 9 | 2 | 2個七邊形 7個矩形 |
D7h, [7,2], (*722), order 28 | 
|
| 八角錐 | 稜錐體 | 
|
( )∨{8} | 9 | 16 | 9 | 2 | 1個八邊形 8個三角形 |
C8v, [8], (*88) | |
| 四角錐柱 | 角錐柱 詹森多面體 |

|
P4+Y4 | 9 | 16 | 9 | 2 | 4個三角形 5個正方形 |
C4v, [4], (*44) | 
|
| 四角錐台錐 | 截角雙錐 | 
|
9 | 16 | 9 | 2 | 1個四邊形 4個梯形 4個三角形 |
C4v, [4], (*44) | 
| |
| 截頂角四方偏方面體 | 截頂角偏方面體 | 
|
13 | 20 | 9 | 2 | 1個正方形 4個五邊形 4個鷂形 |
C4v, [4], (*44) | 
|
扭歪九面體
[编辑]扭歪九面體是指面與頂點並不存在同一個三維空間而無法確定體積的九面體,扭歪九面體僅能存在於四維或以上的空間。
而扭歪九面體的一個例子為四角四片三角孔扭歪正九面體,其由9個正方形組成,可由三角三角柱體柱移除所有三角形面來構造。
參考文獻
[编辑]- ^ Steven Dutch: How Many Polyhedra are There? (页面存档备份,存于互联网档案馆)
- ^ Counting polyhedra (页面存档备份,存于互联网档案馆) numericana.com [2016-1-10]
- ^ Biggs, N.L., T.P. Kirkman, mathematician, The Bulletin of the London Mathematical Society, 1981, 13 (2): 97–120, MR 0608093, doi:10.1112/blms/13.2.97.
- ^ David I. McCooey. Simplest Canonical Polyhedron with D7h Symmetry: Heptagonal Prism. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ David I. McCooey. Simplest Canonical Polyhedron with D7h Symmetry: Heptagonal Dipyramid. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ Wolfram, Stephen. Heptagonal prism. from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ David I. McCooey. Simplest Canonical Polyhedron with C8v Symmetry: Octagonal Pyramid. [2022-09-14]. (原始内容存档于2022-09-14).
- ^ 8.0 8.1 Wolfram, Stephen. "Octagonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Hosoya, Haruo; Nagashima, Umpei; Hyugaji, Sachiko, Topological twin graphs. Smallest pair of isospectral polyhedral graphs with eight vertices, Journal of Chemical Information and Modeling, 1994, 34 (2): 428–431, doi:10.1021/ci00018a033.
- ^ Critchlow, Keith, Order in space: a design source book, Viking Press: 54, 1970.
- ^ Goldberg, Michael, On the space-filling enneahedra, Geometriae Dedicata, 1982, 12 (3): 297–306, doi:10.1007/BF00147314.
| ||||||||||||||||||||||









