一面体
| 部分的一面体 | |
|---|---|
 球面一面体{1,1} |
 环形一面体{4,4}1,0 |
在几何学中,一面体是多面体的一种,是指仅由一个面构成的几何结构。一面体在三维普通空间中是不存在的,但能存在于超球或射影平面等其他结构的空间中。
最简单的一面体是存于球面上的几何结构,等同于一个没有二角形分划的球体,更复杂地,一面体也可以是环面上的正则地区图。在抽象几何学中,二面体半形也是一种一面体。
一面体中并不包括任何锥体和柱体,即使是退化的形式也不存在,因为如果锥体要仅有一个面,其底面必须是零角形且不存在侧面;柱体则是因为柱体有顶面和底面至少需要两个面。
球面多面体
[编辑]
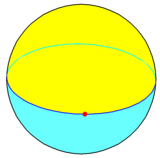
一面体可以以球面多面体的方式存在于球面或超球面上。这类一面体有两种,一种为一面形,即由1个恰好填满整个球面的月牙形或球弓形组成,可以视为底为一角形的多面形,在施莱夫利符号中可以用{2,1}表示[1]。这种一面体共有1个面1条棱和2个顶点,对偶多面体为一角形二面体(施莱夫利符号:{1,2})。
| 一面形 | 一面形的对偶多面体 |
|---|---|
 一面形 施莱夫利符号{2,1} |
 一角形二面体 施莱夫利符号{1,2} |
另一种一面体则以类似一角形存在于圆形上的形式存在于三维球面上,其由单个顶点在球体上,没有边和一个单一个面所组成。一面体的对偶是自己,即自身对偶,即可以换点和面心创造本身作为一个中心的镜射,这种几何结构只有1个面、没有边和1个顶点,在施莱夫利符号中利用{1,1}来表示。
正则地区图
[编辑]一面体可以以正则地区图的方式存在。
环形多面体
[编辑]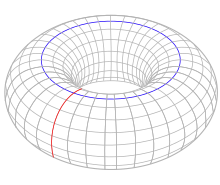

一面体可以以环形多面体的方式存在,例如{4,4}1,0[3]和{6,3}1,0[4]。其中{4,4}1,0由1个正方形组成,共有1个面、2条边和1个顶点、{6,3}1,0由1个正方形组成,共有1个面、3条边和2个顶点。
 {4,4}1,0 由1个面、2条棱和1个顶点组成 (v:1, e:2, f:1) |
 皮特里三面形 {6,3}1,0 由1个面、3条棱和2个顶点组成 (v:2, e:3, f:1) |
此外,以正则地区图表达的无边地区图(edgeless map)也可以视为一种一面体,其施莱夫利符号表示为{0,0},由1个面、0条边和1个顶点组成,是一个自身对偶多面体。[5]
多边形二面体半形
[编辑]多边形二面体半形是一种多面体半形,属于抽象正多面体,有着多边形二面体一半的面。其对应于图论中的循环图。[6]仅有偶数边数的多边形二面体可以存在多面体半形。2p边形二面体半形具有1个面、p条边和p个顶点,亏格为1,在施莱夫莉符号中可以用{2p,2}/2表示。[7][6]
| 名称 | 图 | χ | g | 施莱夫利符号 | 顶点 | 边 | 面 | 群 | 阶数 | 对偶多面体 | 皮特里对偶 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 二角形二面体半形[8] 二面形半形[8] |
C1 | 1 | n1 | {2,2}/2 | 1 | 1 | 1 | Dih2 | 4 | (自身对偶)[8] | 一角形二面体[8] | |
| 正方形二面体半形 | C2 | 1 | n1 | {4,2}/2 | 2 | 2 | 1 | Dih4 | 8 | 四面形半形[9] | (自身对偶)[9] | |
| 六边形二面体半形 | C3 | 1 | n1 | {6,2}/2 | 3 | 3 | 1 | Dih6 | 12 | 六面形半形[10] | 三角形二面体[10] | |
| 八边形二面体半形 | C4 | 1 | n1 | {8,2}/2 | 4 | 4 | 1 | Dih8 | 16 | 八面形半形[11] | (自身对偶)[11] | |
| 十边形二面体半形 | C5 | 1 | n1 | {10,2}/2 | 5 | 5 | 1 | Dih10 | 20 | 十面形半形[12] | 五边形二面体[12] | |
| 十二边形二面体半形 | C6 | 1 | n1 | {12,2}/2 | 6 | 6 | 1 | Dih12 | 24 | 十二面形半形[13] | (自身对偶)[13] | |
参见
[编辑]参考文献
[编辑]- ^ Coxeter, Introduction to geometry, 1969, Second edition, sec 21.3 Regular maps, p. 386-388
- ^ 2.0 2.1 Coxeter, H. S. M.; Moser, W. O. J., Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete 14 4th, Springer Verlag, 1980, ISBN 978-0-387-09212-6
- ^ Coxeter 1980[2], 8.3 Maps of type {4,4} on a torus.
- ^ Coxeter 1980[2], 8.4 Maps of type {3,6} or {6,3} on a torus.
- ^ The edgeless map. Regular Map database - map details. [2021-07-24]. (原始内容存档于2020-08-03).
- ^ 6.0 6.1 Séquin, Carlo. Symmetrical immersions of low-genus non-orientable regular maps (PDF). Berkeley University. [2020-08-14]. (原始内容存档 (PDF)于2015-09-23).
- ^ Regular maps in the non-orientable surface of genus 1. weddslist.com. [2020-08-14]. (原始内容存档于2019-12-28).
- ^ 8.0 8.1 8.2 8.3 The hemi-2-hosohedron. weddslist.com.
- ^ 9.0 9.1 The hemi-di-square. weddslist.com. [2020-08-14]. (原始内容存档于2020-02-01).
- ^ 10.0 10.1 The hemi-di-hexagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
- ^ 11.0 11.1 The hemi-di-octagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
- ^ 12.0 12.1 The hemi-di-decagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
- ^ 13.0 13.1 The hemi-di-dodecagon. weddslist.com. [2020-08-14]. (原始内容存档于2016-03-14).
