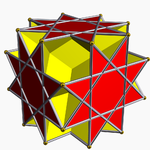
小反平行四边形二十四面体
外观
 | |||
| 类别 | 均匀多面体对偶 星形多面体 | ||
|---|---|---|---|
| 对偶多面体 | 小斜方立方体 | ||
| 识别 | |||
| 名称 | 小反平行四边形二十四面体 | ||
| 参考索引 | DU18 | ||
| 数学表示法 | |||
| 威佐夫符号 | 3/2 2 4|[1] | ||
| 性质 | |||
| 面 | 24 | ||
| 边 | 48 | ||
| 顶点 | 18 | ||
| 欧拉特征数 | F=24, E=48, V=18 (χ=-6) | ||
| 组成与布局 | |||
| 面的种类 | 24个反平行四边形 | ||
| 顶点布局 | 4个反平行四边形的公共顶点 8个反平行四边形的公共顶点 | ||
| 对称性 | |||
| 对称群 | Oh, [4,3], *432 | ||
| 特性 | |||
| 等面、非凸 | |||
| 图像 | |||
| |||
在几何学中,小反平行四边形二十四面体是一种星形二十四面体,由24个反平行四边形组成,其索引编号为DU18[2],对偶多面体为小斜方立方体[3]。其外观与小六角星化二十四面体相同。
性质
[编辑]小反平行四边形二十四面体由24个全等的反平行四边形组成,其具有48条棱和18个顶点[4]。在其18个顶点中,有12个是4个反平行四边形的公共顶点、另外6个是8个反平行四边形的公共顶点[5]。
每个反平行四边形具有2个的角以及2个的角,其对角线交角为。每个边相邻的两个反平行四边形间的二面角皆为。[5]
相关多面体
[编辑]反平行四边形二十四面体
[编辑]小反平行四边形二十四面体由24个全等的反平行四边形组成,其具有48条棱和18个顶点[5],这些特性与反平行四边形二十四面体相同[6],但他们的对偶多面体不同:小反平行四边形二十四面体的对偶多面体为小斜方立方体[3];而反平行四边形二十四面体的对偶多面体为大斜方立方体[7]。
另外一个差别在于其顶点间的相联方式,小反平行四边形二十四面体的顶点图为八边形,而反平行四边形二十四面体顶点图为八角星,根据对偶多面体的定义,对偶多面体的面形状会与原始立体的顶点图相同[8],小斜方立方体由正方形和八边形组成[9],而大斜方立方体由三角形和八角星组成[10]而导致了这些差异。
| 多面体 |  小反平行四边形二十四面体 |
 反平行四边形二十四面体 |
|---|---|---|
| 组成的面 |  反平行四边形 |
 反平行四边形 |
| 对偶多面体 |  小斜方立方体 |
 大斜方立方体 |
小六角星化二十四面体
[编辑]小反平行四边形二十四面体的外观与小六角星化二十四面体相同,但组成面的形状不同:小反平行四边形二十四面体的面由反平行四边形组成,而小六角星化二十四面体的面由凹筝形组成。[11]
| 多面体 |  小反平行四边形二十四面体 |
 小六角星化二十四面体 |
|---|---|---|
| 组成的面 |  反平行四边形 |
 凹筝形 |
| 对偶多面体 |  小斜方立方体 |
 小立方立方八面体 |
参见
[编辑]参考文献
[编辑]- ^ Dual 18: small rhombihexacron. gratrix.net. [2021-09-03]. (原始内容存档于2021-04-01).
- ^ Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208
- ^ 3.0 3.1 Eric W. Weisstein. Small Rhombihexacron. 密歇根州立大学图书馆. [2021-09-03]. (原始内容存档于2013-06-04).
- ^ Vladimir Bulatov. Small Rhombihexacron. [2021-09-03]. (原始内容存档于2020-02-23).
- ^ 5.0 5.1 5.2 David I. McCooey. Versi-Quasi-Regular Duals: Small Rhombihexacron. dmccooey.com. [2019-09-07]. (原始内容存档于2021-09-03).
- ^ Great Rhombihexacron. kitwallace.co.uk. [2021-09-03]. (原始内容存档于2021-09-03).
- ^ Great Rhombihexacron. 密歇根州立大学图书馆. [2019-09-07]. (原始内容存档于2014-07-11).
- ^ Weisstein, Eric W. (编). Dual Polyhedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Small Rhombihexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Great Rhombihexahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Dual 13: small hexacronic icositetrahedron. gratrix.net. [2021-09-03]. (原始内容存档于2021-04-01).






