蛇引理
外观
在同调代数中,蛇引理是构造长正合序列的关键工具,此引理在任何阿贝尔范畴中皆成立。依此构造的同态通常称作连结同态。
叙述
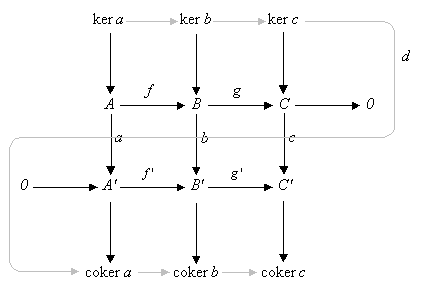
[编辑]使得每一横列均为正合序列。此时存在一个联系的核与上核的正合序列:
引蛇出洞
[编辑]为了理解蛇引理的由来,观察下图:
并注意到:引理给出的正合序列可在此图中画成倒S状的蛇形。
构造连接同态
[编辑]核间的同态与上核间的同态很容易构造,它们由该图的交换性自然导出,正合性也可以直接代定义验证。重点在于连接同态及序列在该处的正合性。
对于模范畴的情形,同态可如是构造:
选定,并视之为的元素;由于是满射,存在满足。由图的交换性,我们有
- (因为)
于是。由于底部的横列正合,存在使得。置。今须验证是明确定义的,即不依赖之选取;此外尚须验证它是个同态,及序列的正合性。
一旦完成以上几点验证,即证明了此引理在模范畴的情形。对一般情形,可利用核与上核的泛性;此外也能使用Mitchell嵌入定理,此定理断言任一阿贝尔范畴都能迁入某个环的-模范畴。
函子性
[编辑]在应用上,我们常常需要长正合列的“函子性”或曰“自然性”(就自然变换意义言之);各种建构的函子性也是同调代数的基本哲学。此函子性可由蛇引理的函子性导出。
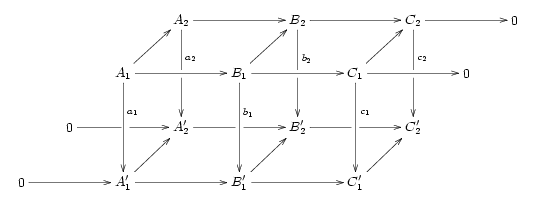
设交换图
的横列均为正合,则可利用蛇引理两次,一次在“前”一次在“后”,产生两条长正合序列;它们经由以下交换图相连系:
文献
[编辑]- Serge Lang, Algebra (2002), Graduate Texts in Mathematics 211, Springer. ISBN 0-387-95385-X