截角五維超正方體

截角五維超正方體
類型	五維均勻多胞體
維度	5
數學表示法
考克斯特符號
施萊夫利符號	t{4,3,3,3}
性質
四維胞	42
胞	200
面	400
邊	400
頂點	160
組成與佈局
頂點圖	Elongated tetrahedral pyramid
對稱性
考克斯特群	BC5, [3,3,3,4]
特性
convex

截角五維超正方體可以通過在每條棱距離頂點$1/({\sqrt {2}}+2)$處截斷五維超正方體的頂點來得到。每個被截斷的頂點會產生一個新的正五胞體。

坐標

一個棱長為2的截角五維超正方體的每個頂點的笛卡兒坐標系坐標為:

$\left(\pm 1,\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}})\right)$

投影

正交投影

考克斯特平面	B5	B4 / D5	B3 / D4 / A2
Graph
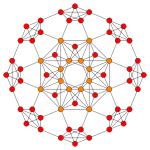
二面體群	[10]	[8]	[6]
考克斯特平面	B2	A3
Graph
二面體群	[4]	[4]

截角五維超正方體是各維度截角超方形中的第四個:

截角超方形

							...
八邊形	截角立方體	截角正八胞體	截角五維超正方體	截角六維超正方體	截角七維超正方體	截角八維超正方體

參考文獻

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] （頁面存檔備份，存於網際網路檔案館）
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. 5D uniform polytopes (polytera). bendwavy.org.  o3o3o3x4x - tan, o3o3x3x4o - bittin

外部連結

• 埃里克·韋斯坦因. Hypercube. MathWorld. 
• Olshevsky, George, Measure polytope at Glossary for Hyperspace.
• Polytopes of Various Dimensions
• Multi-dimensional Glossary （頁面存檔備份，存於網際網路檔案館）