樹旋轉
此條目沒有列出任何參考或來源。 (2015年3月5日) |

在資料結構中,樹旋轉(英語:Tree rotation)是對二元樹的一種操作,不影響元素的順序,但會改變樹的結構,將一個節點上移、一個節點下移。樹旋轉會改變樹的形狀,因此常被用來將較小的子樹下移、較大的子樹上移,從而降低樹的高度、提升許多樹操作的效率。
樹的旋轉方向有很多不同的定義,有些定義彼此之間還存在衝突。有些人認為旋轉方向應該反映節點的移動方向(左子樹旋轉到父節點的位置為右旋),有些人則認為旋轉方向應該反映被旋轉的子樹是哪棵(左子樹旋轉到父節點的位置為左旋,與前一種說法相反)。這篇維基文章採用前者的定義:旋轉方向為節點的移動方向。
圖示
[編輯]
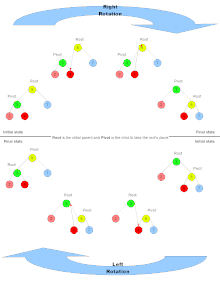
對一棵樹進行旋轉時,這棵樹的根節點是被旋轉的兩棵子樹的父節點,稱為旋轉時的根(英語:root);如果節點在旋轉後會成為新的父節點,則該節點為旋轉時的轉軸(英語:pivot)。
上圖中,樹的右旋操作以 Q 為根、P 為轉軸,會將樹順時針旋轉。相應的逆操作為左旋,會以 Q 為轉軸,將樹逆時針旋轉。
理解樹旋轉過程的關鍵,在於理解其中不變的約束。旋轉操作不會導致葉節點順序的改變(可以理解為旋轉操作前後,樹的中序遍歷結果是一致的),旋轉過程中也始終受二元搜尋樹的主要性質約束:右子節點比父節點大、左子節點比父節點小。尤其需要注意的是,進行右旋轉時,旋轉前根的左節點的右節點(例如上圖中以 Q 為根的 B 節點)會變成根的左節點,根本身則在旋轉後會變成新的根的右節點,而在這一過程中,整棵樹一直遵守著前面提到的幾個約束。相反的左旋轉操作亦然。
如果將根記為 Root、轉軸記為 Pivot、子節點中與旋轉方向相同的一側記為 RS(旋轉側,英語:Rotation Side)、旋轉對側記為 OS(英語:Opposite Side),則上圖中 Q 節點的 RS 為 C、OS 為 P,將其右旋轉的虛擬碼為:
Pivot = Root.OS Root.OS = Pivot.RS Pivot.RS = Root Root = Pivot
該操作為常數時間複雜度。
中序不變
[編輯]二元樹旋轉前後,中序遍歷的結果不變。因此樹的任何部分旋轉,對整棵樹的元素順序沒有影響。上圖中兩棵樹的中序遍歷結果為:
左側的樹: ((A, P, B), Q, C) 右側的樹: (A, P, (B, Q, C))
由兩者其中之一計算另一個很簡單:
如果要將節點 Q 右旋:
設 P 為 Q 的左子樹。 將 Q 的左子樹設為 P 的右子樹。 [將 P 的右子樹的父節點設為 Q] 將 P 的右子樹設為 Q。 [將 Q 的父節點設為 P]
如果要將節點 P 左旋:
設 Q 為 P 的右子樹。 將 P 的右子樹設為 Q 的左子樹。 [將 Q 的左子樹的父節點設為 P] 將 Q 的左子樹設為 P。 [將 P 的父節點設為 Q]
其餘節點間的連接不變。
樹的左右旋轉操作還可以組合執行,稱作雙旋轉(英語:double rotation)。先將 X 的右子樹右旋、再將 X 本身左旋,就是 X 的雙左旋轉(英語:double left rotation)。同理,先將 X 的左子樹左旋、再將 X 本身右旋,就是 X 的雙右旋轉(英語:double right rotation)。
很多樹形資料結構中都用到了樹的旋轉操作,例如AVL樹、紅黑樹、伸展樹、樹堆等。因為是局部變形,只涉及5個節點,不需要檢查整棵樹,所以操作只需要常數時間。
實現
[編輯]上面的圖示僅描述了如何進行局部變換, 在實際應用中, 還需要將原有父節點的父節點納入考慮範圍. 以上述右旋轉為例, 如果 Q 是其父節點 root 的左子節點, 則在旋轉完後 root 的左子節點需要修改指向節點 P. 但這一點並沒有體現在上面的圖示中.
在接下來的實現中, 假設從樹中任一節點 N 能夠藉由 N.left 訪問其左子節點, N.right 訪問其右子節點, N.parent 訪問其父節點. 此外, 稱旋轉後變為父親的節點為轉軸 pivot, 稱 pivot 在旋轉前的父節點為 parent, 而 parent 在旋轉前的父節點為 root. 則右旋轉過程可用虛擬碼表示為
func rotate_right(pivot):
let parent = pivot.parent
let root = parent.parent
// R0
parent.left = pivot.right
if pivot.right != nil: pivot.right.parent = parent
// R1
pivot.parent = root
if parent == root.left:
root.left = pivot
else:
root.right = pivot
pivot.right = parent
parent.parent = pivot
而左旋轉可表示為
func rotate_left(pivot):
let parent = pivot.parent
let root = parent.parent
// L0
parent.right = pivot.left
if pivot.left != nil: pivot.left.parent = parent
// L1
pivot.parent = root
if parent == root.left:
root.left = pivot
else:
root.right = pivot
pivot.left = parent
parent.parent = pivot
上述過程並不適用於當 parent 節點本身就是樹的根節點的情況. 這種情況下, 需要以其它方式重設樹的根節點為 pivot. 一種無需在根節點的某一子節點為轉軸時進行特殊處理的替代方案是讓樹的實際的根節點是一個特殊入口節點, 而邏輯上的根節點作為該入口節點的某個子節點存在, 並避免任何以邏輯根節點為轉軸的旋轉.
如果從節點出發, 只能訪問其兩個子節點, 而無法訪問其父節點, 那麼上述方法也不適用. 這種情況下, root 節點亦是旋轉的必要參數之一. 旋轉過程的虛擬碼表示如下
func rotate_right(root, parent):
assert root.left == parent || root.right == parent
let pivot = parent.left
// R0
parent.left = pivot.right
// R1
if parent == root.left:
root.left = pivot
else:
root.right = pivot
pivot.right = parent
func rotate_left(root, parent):
assert root.left == parent || root.right == parent
let pivot = parent.right
// L0
parent.right = pivot.left
// L1
if parent == root.left:
root.left = pivot
else:
root.right = pivot
pivot.left = parent
旋轉距離
[編輯]兩棵二元樹之間的旋轉距離指的是, 其中一棵樹通過儘可能少的樹旋轉變換到另一棵樹的過程中所需要的旋轉次數. 對於一個包含相同個數節點的二元樹集合, 它們兩兩之間的距離可以構成一個度量空間. 是否存在一個演算法, 能在多項式時間內計算兩個二元樹之間的旋轉距離, 目前還是未解決問題.
參考文獻
[編輯]Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms. Massachusetts: The MIT Press, 2002. pp273-77. ISBN 0-07-013151-1

