逆序对

这个置换中的一个逆序对，可以由位置对（2,4）或元素对（5,2）表示。这个置换的逆序，可以使用基于元素表示法，表示为：(3, 1), (3, 2), (5, 1), (5, 2)和(5,4)。

在计算机科学和离散数学中，一个序列的逆序（inversion）对，是失去自然次序的元素对。

定義

逆序

設$\pi$為一個排列，如果$i<j$而且$\pi (i)>\pi (j)$， 這個序位$(i,j)$或這一對元素${\bigl (}\pi (i),\pi (j){\bigr )}$，被稱為是$\pi$的一個逆序。通常逆序是對於排列的定義，但也可以用於序列：

設$S$是一個序列（或多重排列）。如果$i<j$而且$S(i)>S(j)$， 這個序位$(i,j)$或這對元素${\bigl (}S(i),S(j){\bigr )}$，被稱為是$S$的一個逆序。

對於根據元素組成的序列，逆序的定義不是唯一的，因為不同的序位上可能有相同的值對。逆序集是所有逆序的集合。一個排列依其序位而定義的逆序集是，它的反向排列依其序位而定義的逆序集，反之亦然，只是交換了配對的元素。

逆序數

一个序列$X=\langle x_{1},\dots ,x_{n}\rangle$的逆序數${\mathtt {inv}}(X)$，是逆序集的基數，它常用於量度排列或序列的已排序程度。

在一個排列的箭頭指向圖中，它是箭頭指向相交叉的數，也是從自指(identity)排列而得到的Kendall tau距離，以及每個反向相關向量的和，如下列定義。

對於逆序數，依序位或依元素而定義的分別並不重要，因為排列及其反向排列都具有相同的逆序數。

其它測量（預先）排序程度的方式，包括了為排好序列而從序列中可以刪除元素的最小數量，對序列所“進行”排序的次數和長度，每個元素在已排序位置之上的距離總和（Spearman footrule），以及排序過程中必需的最少交換次數。比較排序算法計算逆序數的時間為O(n log n)。

目前求逆序对数目比较普遍的方法是利用归并排序做到$O(n\log n)$的时间复杂度。当然，也可以利用树状数组、线段树来实现这种基础功能。复杂度均为$O(n\log n)$。

相關聯的逆序向量

有三個類似的向量用於將排列的逆序，壓縮到確定唯一的向量中。它們通常被稱為逆序向量或Lehmer碼。本文將逆序向量記為($v$)，其它的兩個向量有時分別稱為左和右逆序向量；為了避免與前面的逆序向量混淆，本文將另兩個分別稱為左逆序計數$l$和右逆序計數$r$。左逆序計數是以反向colexicographic次序的排列，右逆序計數則是以字典次序的排列。

Rothe diagram

• 逆序向量$v$：依據元素的定義，$v(i)$是較小（右）分量為$i$的逆序數。$v(i)$是在$\pi$之中的$i$之前，元素較$i$大的數量。

  $v(i)~~=~~\#\{k\mid k>i~\land ~\pi ^{-1}(k)<\pi ^{-1}(i)\}$

• 左逆序計數$l$：依據位置的定義，$l(i)$是較大（右）分量為$l(i)$的逆序數。$l(i)$是在$\pi (i)$之中的$\pi (i)$之前，元素較$\pi (i)$大的數量。

  $l(i)~~=~~\#\left\{k\mid k<i~\land ~\pi (k)>\pi (i)\right\}$

• 右逆序計數$r$，通常稱為Lehmer碼：依據位置的定義，$r(i)$是較小（左）分量為i的逆序數。$r(i)$是$\pi (i)$之中的$\pi (i)$之後，元素較$\pi (i)$小的數量。

  $r(i)~~=~~\#\{k\mid k>i~\land ~\pi (k)<\pi (i)\}$

Rothe圖可以協助找出$v$和$r$。Rothe圖是以黑點來表示1的排列矩陣，每一個位置上若為逆序（通常以叉號表示）則在其右側與下方即有一點。$r(i)$是圖中第$i$列排列逆序的加總，而$v(i)$是$i$欄中排列逆序的加總。排列矩陣的倒反即是此矩陣的轉置，因此某一排列的$v$即是它轉置的$r$，反之亦然。

範例：四個元素的全部排列

四個元素可能的6種排列

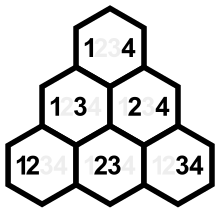
下面可排序表顯示了四個元素的集合，它的逆序集會有不同位置的24種排列、逆序相關向量和逆序數（右欄是它的反向排列，用於以colex排序）。可以看出$v$和$l$的位數總是相同，而$l$和$r$與位逆序集有關。 最右側欄是排列左上右下對角線的總和，如三角形圖示，以及r是左下右上對角線的總和（配對在下降對角線中其右側都是2,3,4組成，而在上升對角線中的左側都是1,2,3組成）。 此表中$\pi$的預設排序是反向colex次序，這與$l$的colex次序相同。$\pi$的字典序與$r$的字典序相同。

三個元素的全部排列表
0 1 2 3 4 5 $\pi$ $v$ $l$ p-b $r$ # 0 123 321 000 000 000 000 000 000 0 1 213 312 100 001 010 010 100 001 1 2 132 231 010 010 100 001 010 010 1 3 312 213 110 011 110 011 200 002 2 4 231 132 200 002 200 002 110 011 2 5 321 123 210 012 210 012 210 012 3

四個元素的全部排列表

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 $\pi$ $v$ $l$ p-b $r$ # 0 1234 4321 0000 0000 0000 0000 0000 0000 0 1 2134 4312 1000 0001 0010 0100 1000 0001 1 2 1324 4231 0100 0010 0100 0010 0100 0010 1 3 3124 4213 1100 0011 0110 0110 2000 0002 2 4 2314 4132 2000 0002 0200 0020 1100 0011 2 5 3214 4123 2100 0012 0210 0120 2100 0012 3 6 1243 3421 0010 0100 1000 0001 0010 0100 1 7 2143 3412 1010 0101 1010 0101 1010 0101 2 8 1423 3241 0110 0110 1100 0011 0200 0020 2 9 4123 3214 1110 0111 1110 0111 3000 0003 3 10 2413 3142 2010 0102 1200 0021 1200 0021 3 11 4213 3124 2110 0112 1210 0121 3100 0013 4 12 1342 2431 0200 0020 2000 0002 0110 0110 2 13 3142 2413 1200 0021 2010 0102 2010 0102 3 14 1432 2341 0210 0120 2100 0012 0210 0120 3 15 4132 2314 1210 0121 2110 0112 3010 0103 4 16 3412 2143 2200 0022 2200 0022 2200 0022 4 17 4312 2134 2210 0122 2210 0122 3200 0023 5 18 2341 1432 3000 0003 3000 0003 1110 0111 3 19 3241 1423 3100 0013 3010 0103 2110 0112 4 20 2431 1342 3010 0103 3100 0013 1210 0121 4 21 4231 1324 3110 0113 3110 0113 3110 0113 5 22 3421 1243 3200 0023 3200 0023 2210 0122 5 23 4321 1234 3210 0123 3210 0123 3210 0123 6

排列的弱次序

对称群的Permutohedron S₄

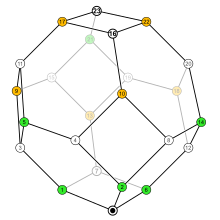
n物品排列的集合其部份次序的結構，稱為排列的弱次序，而構成格。 以逆序集的子集關係繪出的哈斯圖，則構成了稱為permutohedron的骨架。 如果依位置將某一排列分配給每個逆序集，所得到的排序是permutohedron的次序，其中的邊對應於連續兩元素的交換。這是排列的弱排序。The identity is its minimum, and the permutation formed by reversing the identity is its maximum. 如果依元素將某一排列分配給每個逆序集，所得到的排序將是凱萊圖的次序，其中的邊對應於連續兩元素的交換。對稱組的凱萊圖與其permutohedron相似，但是每個排列由其反向替換。

引用

参考书目

• Aigner, Martin. Word Representation. A course in enumeration. Berlin, New York: Springer. 2007. ISBN 978-3642072536. 
• Barth, Wilhelm; Mutzel, Petra. Simple and Efficient Bilayer Cross Counting. Journal of Graph Algorithms and Applications. 2004, 8 (2): 179–194. doi:10.7155/jgaa.00088 . 
• Bóna, Miklós. 2.2 Inversions in Permutations of Multisets. Combinatorics of permutations. Boca Raton, FL: CRC Press. 2012. ISBN 978-1439850510. 
• Comtet, Louis. 6.4 Inversions of a permutation of [n]. Advanced combinatorics; the art of finite and infinite expansions. Dordrecht,Boston: D. Reidel Pub. Co. 1974. ISBN 9027704414. 
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. Introduction to Algorithms 2nd. MIT Press and McGraw-Hill. 2001. ISBN 0-262-53196-8. 
• Gratzer, George. 7-2 Basic objects. Lattice theory. special topics and applications. Cham, Switzerland: Birkhäuser. 2016. ISBN 978-3319442358. 
• Kleinberg, Jon; Tardos, Éva. Algorithm Design. 2005. ISBN 0-321-29535-8. 
• Knuth, Donald. 5.1.1 Inversions. The Art of Computer Programming. Addison-Wesley Pub. Co. 1973. ISBN 0201896850. 
• Mahmoud, Hosam Mahmoud. Sorting Nonrandom Data. Sorting: a distribution theory. Wiley-Interscience series in discrete mathematics and optimization 54. Wiley-IEEE. 2000. ISBN 978-0-471-32710-3. 
• Pemmaraju, Sriram V.; Skiena, Steven S. Permutations and combinations. Computational discrete mathematics: combinatorics and graph theory with Mathematica. Cambridge University Press. 2003. ISBN 978-0-521-80686-2. 
• Vitter, J.S.; Flajolet, Ph. Average-Case Analysis of Algorithms and Data Structures. van Leeuwen, Jan (编). Algorithms and Complexity 1 2nd. Elsevier. 1990. ISBN 978-0-444-88071-0. 

延伸阅读

• Margolius, Barbara H. Permutations with Inversions. Journal of Integer Sequences. 2001, 4. 

预排序措施

• Mannila, Heikki. Measures of presortedness and optimal sorting algorithms. IEEE Transactions on Computers. April 1985, C–34 (4): 318–325. doi:10.1109/tc.1985.5009382. 
• Estivill-Castro, Vladimir; Wood, Derick. A new measure of presortedness. Information and Computation. 1989, 83 (1): 111–119. doi:10.1016/0890-5401(89)90050-3 . 
• Skiena, Steven S. Encroaching lists as a measure of presortedness. BIT. 1988, 28 (4): 755–784. S2CID 33967672. doi:10.1007/bf01954897.