二项堆

在计算机科学中，二项堆（binomial heap）是一种类似于二叉堆的堆结构。与二叉堆相比，其优势是可以快速合并两个堆，因此它属于可合并堆（mergeable heap）抽象数据类型的一种。

二项树 [编辑]

二项树是一种通过递归定义的有序树，可以由以下定义得到：

度数为0的二项树只包含一个结点
度数为k的二项树有一个根结点，根结点下有 $k$ 个子女，每个子女分别是度数为 $k-1, k-2, ..., 2, 1, 0$ 的二项树的根

二项树（从左至右度数分别为0至3

度数为k的二项树共有 $2^k$ 个结点，高度为 $k$ 。在深度d处有 $\tbinom n d$ （二项式系数）个结点。

二项堆 [编辑]

二项堆是指满足以下性质的二项树的集合：

每棵二项树都满足最小堆性质，即结点关键字大于等于其父结点的关键字
不能有两棵或以上的二项树有相同度数（包括度数为0）

以上第一个性质保证了二项树的根结点包含了最小的关键字。第二个性质则说明结点数为 $n$ 的二项堆最多只有 $\log{n} + 1$ 棵二项树。

示例：一个含13个结点的二项堆

二项堆的操作 [编辑]

由于并不需要对二项树的根结点进行随机存取，因而这些结点可以存成链表结构。

合并 [编辑]

合并度数相同的二项树

合并二项堆

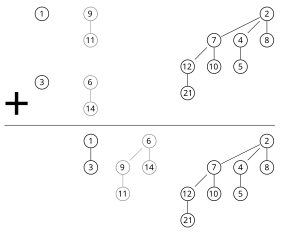
最基本的为二个度数相同的二项树的合并。由于二项树根结点包含最小的关键字，因此在二颗树合并时，只需比较二个根结点关键字的大小，其中含小关键字的结点成为结果树的根结点，另一棵树则变成结果树的子树。

function mergeTree(p, q)
    if p.root <= q.root
        return p.addSubTree(q)
    else
        return q.addSubTree(p)

两个二项堆的合并则可按如下步骤进行：度数 $j$ 从小取到大，在两个二项堆中如果其中只有一棵树的度数为 $j$ ，即将此树移动到结果堆，而如果只两棵树的度数都为 $j$ ，则根据以上方法合并为一个度数为 $j+1$ 的二项树。此后这个度数为 $j+1$ 的树将可能会和其他度数为 $j+1$ 的二项树进行合并。

此操作的时间复杂度为 ${O}(\log n)$ 。

插入 [编辑]

创建一个只包含要插入关键字的堆，再将此堆与原先的二项堆进行合并，即可得到插入后的堆。由于需要合并，插入操作需要 ${O}(\log n)$ 的时间。

查找最小关键字所在结点 [编辑]

由于满足最小堆性质，只需查找二项树的的根结点即可，故需要时间为 ${O}(\log n)$ 。

删除最小关键字所在结点 [编辑]

先找到最小关键字所在结点，然后将它从其所在的二项树中删除，并获得其子树。将这些子树看作一个独立的二项堆，再将此堆合并到原先的堆中即可。由于每棵树最多有 $\log n$ 棵子树，创建新堆的时间为 ${O}(\log n)$ 。同时合并堆的时间也为 ${O}(\log n)$ ，故整个操作所需时间为 ${O}(\log n)$ 。

function deleteMin(heap)
    min = heap.trees().first()
    for each current in heap.trees()
        if current.root < min then min = current
    for each tree in min.subTrees()
        tmp.addTree(tree)

减小关键字的值 [编辑]

在减小关键字的值后，可能会不满足最小堆性质。此时，将其所在结点与父结点交换关键字，如还不满足最小堆性质则再与祖父结点交换关键字……直到最小堆性质得到满足。操作所需时间为 ${O}(\log n)$ 。

删除 [编辑]

将需要删除的结点的关键字的值减小到负无穷大（比二项堆中的其他所有关键字的值都小即可），再删除最小关键字的结点即可。

运行时间 [编辑]

以下对于二项堆操作的运行时间都为 ${O}(\log n)$ （结点数为 $n$ ）：

在二项堆中插入新结点
查找最小关键字所在结点
从二项堆中删除最小关键字所在结点
减小给定结点关键字的值
删除给定结点
合并两个二项堆

参见 [编辑]

斐波那契堆

参考资料 [编辑]

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein（潘金贵等译）. 《算法导论》. 机械工业出版社.
Vuillemin, J. (1978). A data structure for manipulating priority queues. Communications of the ACM 21, 309–314.

外部链接 [编辑]

二项堆

目录