莫雷角三分線定理

在欧几里得幾何中,莫雷角三分線定理(Morley's theorem)說明對所有的三角形,其三個内角作角三分線,靠近公共边三分線的三個交點,是一個等邊三角形。此定理由法蘭克·莫雷在1899年發現。对外角作外角三分線,也會有类似的性质,可以再作出4個等邊三角形。
此定理沒辦法用尺規作圖作出其等邊三角形,因為已經證明出尺規作圖無法作出三等分角。
證明[编辑]
引理[编辑]
引理證明[编辑]
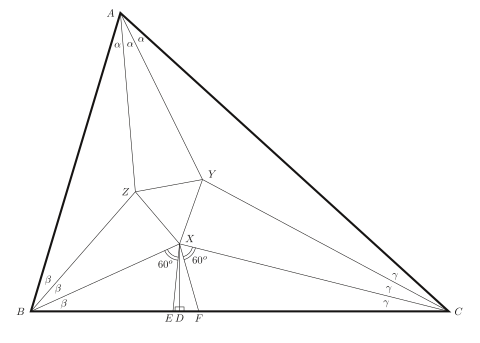
定理證明[编辑]
在中:
- 是的三等分角
- 是的三等分角
- 是的三等分角
作6條角三分線分別為、、、、、,作、、在上,且、
容易得出,由此等式還可以得出以下三式:
由正弦定理可得出:
從這裡可以得出的三個內角,計算出和的正弦值:
我們知道:
從引理我們可以得出:
化簡後得出:
因為和相似,所以可得出:
同理可得出:
綜合以上結果,可得出,因此是等邊三角形
推廣[编辑]
更一般的莫雷角三分線定理由Taylor和Marr於1914年發表,將6條角三分線順時鐘和逆時鐘旋轉120°,其交點共可得出27個不同的等邊三角形。
參見[编辑]
參考資料[编辑]
- Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 253-256, 1929.
- Morley's Miracle — Several proofs of Morley's theorem (页面存档备份,存于互联网档案馆)
- Morleys Theorem (页面存档备份,存于互联网档案馆) MathWorld
- Morley's Trisection Theorem MathPages
















































