红色曲线是龙格函数,蓝色曲线是 5 阶多项式,绿色曲线是 9 阶多项式。随着阶次的增加,误差逐渐变大 在数值分析 领域中,龙格现象 是在一组等间插值点上使用具有高次多项式的多项式插值时出现的区间边缘处的振荡问题。 它是由卡尔·龙格 (Carl Runge)在探索使用多项式插值逼近某些函数时的错误行为时发现的。[1]
魏尔斯特拉斯逼近定理 表明,对于定义在区间
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
{\displaystyle f(x)}
P
n
(
n
=
0
,
1
,
2
,
.
.
.
)
{\displaystyle P_{n}(n=0,1,2,...)}
[
a
,
b
]
{\displaystyle [a,b]}
f
(
x
)
{\displaystyle f(x)}
lim
n
→
∞
(
max
a
≤
x
≤
b
|
f
(
x
)
−
P
n
(
x
)
|
)
=
0.
{\displaystyle \lim _{n\rightarrow \infty }\left(\max _{a\leq x\leq b}\left|f(x)-P_{n}(x)\right|\right)=0.}
考虑使用通过那些点的
n
{\displaystyle n}
P
n
(
x
)
{\displaystyle P_{n}(x)}
f
(
x
)
{\displaystyle f(x)}
n
+
1
{\displaystyle n+1}
f
(
x
)
{\displaystyle f(x)}
P
n
(
x
)
{\displaystyle P_{n}(x)}
随着
n
{\displaystyle n}
P
n
(
x
)
{\displaystyle P_{n}(x)}
f
(
x
)
{\displaystyle f(x)}
[2]
考虑以下龙格函数 :
f
(
x
)
=
1
1
+
25
x
2
{\displaystyle f(x)={\frac {1}{1+25x^{2}}}\,}
龙格发现如果使用
≤
n
{\displaystyle \leq n}
P
n
(
x
)
{\displaystyle P_{n}(x)}
x
i
=
−
1
+
(
i
−
1
)
2
n
,
i
∈
{
1
,
2
,
…
,
n
+
1
}
{\displaystyle x_{i}=-1+(i-1){\frac {2}{n}},\qquad i\in \left\{1,2,\dots ,n+1\right\}}
这样的等距点x i 插值 ,那么在接近端点 −1 与 1 的地方插值结果就会出现震荡。
可以证明,在多项式的阶数增高时插值误差甚至会趋向无限大:
lim
n
→
∞
(
max
−
1
≤
x
≤
1
|
f
(
x
)
−
P
n
(
x
)
|
)
=
∞
{\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty }
解决龙格现象的办法 [ 编辑 ] 使用切比雪夫节点 样条 可以避免这个问题。如果要减小插值误差,那么可以增加构成样条的多项式的数目,而不必是增加多项式的阶次。
参考文献 [ 编辑 ]
^ Runge, Carl , Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten, Zeitschrift für Mathematik und Physik, 1901, 46 : 224–243. www.archive.org ^ Epperson, James. On the Runge example . Amer. Math. Monthly. 1987, 94 : 329–341 [2018-04-27 ] . doi:10.2307/2323093 存档 于2020-09-25).
与正弦基函数吉布斯现象 的比较
《数值分析》,清华大学出版社,李庆扬等编,书号ISBN 978-7-302-18565-9 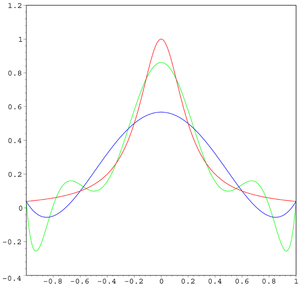

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)









