三角不等式

在三角形中，两条边的长度之和总是大于第三边。

证明所用的三角形

三角不等式是數學上的一個不等式，表示從A到B再到C的距離永不少於從A到C的距離；亦可以說是兩項獨立物件的量之和不少於其和的量。它除了適用於三角形之外，還適用於其他數學範疇及日常生活中。

几何[编辑]

标量[编辑]

在三角形ABC中，这个式子用标量可以写作 ${\overline {AB}}+{\overline {BC}}\geq {\overline {AC}}$ 。

当该式取不等号时，可以由欧几里得第五公设导出；欧几里得给出的证明记载于《几何原本》第一卷命题20：（证明所用的辅助图像见右）^[1]

现在，我们有三角形ABC。延长 ${\overline {AB}}$ 至点D，并使 ${\overline {BD}}={\overline {BC}}$ ，联结 ${\overline {DC}}$ 。

那么，三角形BCD为等腰三角形，所以 $\angle BDC=\angle BCD$ 。记它们均为 $\alpha$ 。

根据欧几里得第五公设，角 $\beta$ 也就是 $\angle ACD$ 大于角 $\alpha$ （ $\angle BCD$ ，也就是 $\angle BDC$ ）；

由于角 $\beta$ 对应边 ${\overline {AD}}$ ，角 $\alpha$ 对应边 ${\overline {AC}}$ ，因此 ${\overline {AD}}>{\overline {AC}}$ （大角对大边，命题19）。^[2]

又由于 ${\overline {DB}}={\overline {BC}}$ ，所以 ${\overline {AD}}={\overline {AB}}+{\overline {BD}}={\overline {AB}}+{\overline {BC}}>{\overline {AC}}$ ，即证。

如果我们将该式左右各减去 ${\overline {BC}}$ ，便能得到 ${\overline {AB}}>{\overline {AC}}-{\overline {BC}}$ ，这便是三角不等式的另一种表达方法：三角形的两边之差小于第三边。

当该式取等号的时候，其已经不属于欧氏几何的范畴，这种情况只有可能在球面三角形中出现，此时 $\left|a-b\right|\leq c\leq a+b$ ，而a, b, c为三角形三边的长。

向量[编辑]

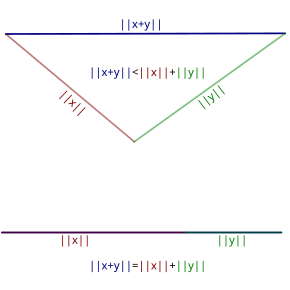
用向量的写法，这个不等式可以写成：

\left|{\overrightarrow {AC}}\right|\leq \left|{\overrightarrow {AB}}\right|+\left|{\overrightarrow {BC}}\right|

上式和标量的写法明显是等价的。

考虑到 ${\overrightarrow {AB}}+{\overrightarrow {BC}}={\overrightarrow {AC}}$ ，该式也可以写成： $\left|{\overrightarrow {AB}}+{\overrightarrow {BC}}\right|\leq \left|{\overrightarrow {AB}}\right|+\left|{\overrightarrow {BC}}\right|$ ，这种情况的形式和下方实数中的形式是一致的。

如果根据向量构建平面直角坐标系，则可以用代数的方式予以证明。

还是以右图中的三角形为例子。假设在坐标系中，向量 ${\overrightarrow {AB}}$ 的方向向量为 $(x_{1},y_{1})$ ，向量 ${\overrightarrow {BC}}$ 的方向向量为 $(x_{2},y_{2})$ ，

那么因为 ${\overrightarrow {AB}}+{\overrightarrow {BC}}={\overrightarrow {AC}}$ ，得向量 ${\overrightarrow {AC}}$ 的方向向量为 $(x_{1}+x_{2},y_{1}+y_{2})$ 。

因此， $\left|{\overrightarrow {AB}}\right|+\left|{\overrightarrow {BC}}\right|={\sqrt {x_{1}^{2}+y_{1}^{2}}}+{\sqrt {x_{2}^{2}+y_{2}^{2}}}$ ， $\left|{\overrightarrow {AC}}\right|={\sqrt {(x_{1}+x_{2})^{2}+(y_{1}+y_{2})^{2}}}$ 。

所以， $\left|{\overrightarrow {AB}}\right|+\left|{\overrightarrow {BC}}\right|-\left|{\overrightarrow {AC}}\right|=2{\sqrt {x_{1}^{2}x_{2}^{2}+x_{1}^{2}y_{2}^{2}+x_{2}^{2}y_{1}^{2}+y_{1}^{2}y_{2}^{2}}}-2x_{1}x_{2}-2y_{1}y_{2}$ 。

而 $(2{\sqrt {x_{1}^{2}x_{2}^{2}+x_{1}^{2}y_{2}^{2}+x_{2}^{2}y_{1}^{2}+y_{1}^{2}y_{2}^{2}}})^{2}=4x_{1}^{2}x_{2}^{2}+4x_{1}^{2}y_{2}^{2}+4x_{2}^{2}y_{1}^{2}+4y_{1}^{2}y_{2}^{2}$ ， $(2x_{1}x_{2}+2y_{1}y_{2})^{2}=4x_{1}^{2}x_{2}^{2}+8x_{1}x_{2}y_{1}y_{2}+4y_{1}^{2}y_{2}^{2}$ ，

两者相减再配方，得到 $(2x_{1}y_{2}-2x_{2}y_{1})^{2}$ ，该式实际上是 $(\left|{\overrightarrow {AB}}\right|+\left|{\overrightarrow {BC}}\right|)^{2}-(\left|{\overrightarrow {AC}}\right|)^{2}$ 的值。

当且仅当 $x_{1}y_{2}=x_{2}y_{1}$ 时，该式的值为0，而此时我们可以推出 $x_{1}=kx_{2},y_{1}=ky_{2},k\in \Re$ ，这说明 $x_{1}$ 和 $x_{2}$ 、 $y_{1}$ 和 $y_{2}$ 都是平行的。而由于 $x_{1}$ ，也就是向量 ${\overrightarrow {AB}}$ 的终点和 $x_{2}$ ，也就是向量 ${\overrightarrow {BC}}$ 的起点是相同的，显然 ${\overrightarrow {AB}}$ 和 ${\overrightarrow {BC}}$ 共线。这种情况在欧氏几何中是不可能的，只有在非欧几何的情况下才能成立。用 $y_{1}$ 和 $y_{2}$ 平行也一样能够推出 ${\overrightarrow {AB}}$ 和 ${\overrightarrow {BC}}$ 共线。