光度

光度在科學的不同領域中有不同的意義。

光度學

黑色曲线为亮适应光度函数曲线，绿色曲线为暗适应光度函数曲线。实线为CIE 1931标准。断续线为1978年修正数据。点线为2005年修正数据。横坐标单位为nm。

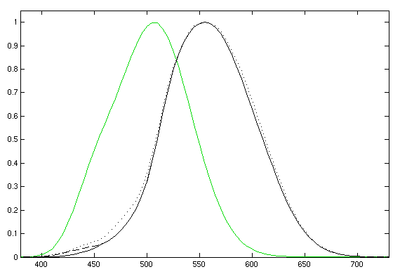
在光度学(photometry)中，"光度"(luminosity)经常与亮度(luminance)弄混。亮度(luminance)是光源在给定方向上单位面积单位立体角内所发出的的光通量，单位是尼特。光度(luminosity)并不是一个物理量，这个词用于"光度函数"(luminosity function)。

人眼能相当精确地判断两种颜色的光亮暗感觉是否相同。所以为了确定眼睛的光谱响应，可将各种波长的光引起亮暗感觉所需的辐射通量进行比较。在较明亮环境中人的视觉对波长为555.016nm的绿色光最为敏感。设任意波长为$\lambda$的光和波长为555.016nm的光产生同样亮暗感觉所需的辐射通量分别为$\Psi_{555.016}$和$\Psi_{\lambda}$，把后者和前者之比

$V(\lambda)=\frac{\Psi_{555.016}}{\Psi_{\lambda}}$

叫做光度函数(luminosity function)或视见函数(visual sensitivity function)。例如，实验表明，1mW的555.0nm绿光与2.5W的400.0nm紫光引起的亮暗感觉相同。于是在400.0nm的光度函数值为

$V(400.0nm)=\frac{10^{-3}}{2.5}=0.0004.$

衡量光通量的大小，要以光度函数为权重把辐射通量折合成对人眼的有效数量。对波长为$\lambda$的光，辐射强度为$\psi(\lambda)$，光通量为$\Phi_v$，则有

$\Phi_v=K_{max} \int V(\lambda)\psi(\lambda)d\lambda$

式中$K_{max}$是波长为555.016nm的光功当量，也叫做最大光功当量，其值为683 lm/W。

天文學

在天文學中，光度(luminosity)是物體每單位時間內輻射出的總能量，即辐射通量，在國際單位是瓦特(Watt)，在厘米克秒制中是“爾格/秒”，天文学常以太陽光度來表示。$L_{\bigodot}$；也就是以太陽的輻射通量為一個單位來表示。太陽的光度是3.846×10²⁶ 瓦特。光度以可指辐射通量的谱分布(spectral luminosity), 单位为瓦特/赫兹(W/Hz)或瓦特/纳米(W/nm)。

光度是與距離無關的物理量，而人眼观看到的天体的亮度（实际上是照度）則明顯的與距離有關，而且是與距離的平方成反比，通常會以視星等來量度。

在測量恆星的亮度時，光度、視星等和距離是相關的參數。如果你已經知道其中的兩項，就可以算出第三項。因為太陽的光度是一個標準值，以太陽的視星等和距離做為這些參數的比較標準，就很容易完成彼此之間的轉換。

光度和亮度之間的計算

點光源S向所有的方向輻射光線。穿越面積A的總量會隨著與光源的距離改變而改變。

假設 $L$ 是一個點光源的光度(即辐射通量)，它向四周輻射的能量是均等的。這個點光源被安置在一個中空球殼的中心，則輻射的所有能量都將穿過這個球殼。當半徑增加時，球殼的表面積也將增加，但通過球殼的光度是恆定不變的，所以將導致在球殼上觀察到的亮度 $b$ 下降。

$b = \frac{L}{A}$ ，此處 $A$ 是被照亮的球殼表面積。 對恆星和一個點光源而言，$A = 4\pi r^2$ 所以 $b = \frac{L}{4\pi r^2} \,$ ，此處 $r$ 是點光源與觀測者的距離。

曾經說明過恆星的光度 $L$ (假設恆星是一個黑體，這僅是一個良好的近似值) 與溫度 $T$ 和半徑 $R$ 的關聯，以方程式表示為：

$L = 4\pi R^2\sigma T^4$ ，此處 σ 是斯特凡-波茲曼常數 5.67×10⁻⁸ W·m^-2·K^-4

除以太陽光度 $L_{\bigodot}$ 和消除常數之後，我們得到如下的關係：

$\frac{L}{L_{\bigodot}} = {\left ( \frac{R}{R_{\bigodot}} \right )}^2 {\left ( \frac{T}{T_{\bigodot}} \right )}^4$.

對一顆主序星，光度也與質量相關：

$\frac{L}{L_{\bigodot}} \sim {\left ( \frac{M}{M_{\bigodot}} \right )}^{3.9}$

這就很容易知道恆星的光度、溫度、半徑和質量之間都是有關聯的。

恆星的星等與亮間是對數的關係，視星等是從地球上觀察到的亮度，絕對星等是在10秒差距上的視星等。 只要知道光度，我們就可以計算在任一給定距離上的視星等：

$m_{\rm star}=m_{\rm sun}-2.5\log_{10}\left({ L_{\rm star} \over L_{\bigodot} } \cdot \left(\frac{ r_{\rm sun} }{ r_{\rm star} }\right)^2\right)$

，此處

m_star 是恆星的視星等(一個純數字)

m_sun 是太陽的視星等(也是一個純數字)

L_star 是恆星的光度

$L_{\bigodot}$ 是太陽的光度

r_star 是到恆星的距離

r_sun 是到太陽的距離

很簡單的，讓 m_sun = −26.73， r_sun = 1.58 × 10⁻⁵ 光年:

m_star = − 2.72 − 2.5 · log(L_star/dist_star²)

例如：

天狼星的光度是多少？

天狼星的距離是8.6光年，星等為−1.47。

Lum(天狼星) = 0.0813 · 8.6² · 10^{−0.4·(−1.47)} = 23.3 × $L_{\bigodot}$

我們可以說天狼星的光度是太陽的23倍，或是它輻射出23倍太陽光度的能量。

一顆熱星等為−10的明亮恆星的光度是10⁶ $L_{\bigodot}$，而熱星等+17等星的暗星光度是10⁻⁵ $L_{\bigodot}$。注意絕對星等可以直接與光度對應，但視星等則是距離的函數。因為只有視星等可以經由觀測直接測量，而有了估計的距離才能確定目標的光度。

散射理論和加速器物理

在散射理論和加速器，光度是在單位時間內在標靶的單位面積上所吸收的粒子數目，在cgs單位制下的因次為公分 ^-2 秒^-1 或b^-1 s^-1 ，光度的累積是光度對時間的積分。光度是描述加速器性能和特性的重要數值。

與光度有關的元素

• $L$ 是光度
• $N$ 是參與反應的數目。
• $\rho$ 是在每一束粒子束內的粒子密度。
• $\sigma$ 是全部的有效截面積。
• $d\Omega$ 是微分的 立體角.
• $\left(\frac{d\sigma}{d\Omega}\right)$是微分的有效截面積 。

於是有下列的關係存在：

$L = \rho v$ (如果標靶是理想的非導體)

$\frac{dN}{dt} = L \sigma$

$\left(\frac{d\sigma}{d\Omega}\right) = \frac{1}{L} \frac{d^{2}N}{d\Omega dt}$

對一個相交的儲存環對撞機：

• $f$ 是交流頻率
• $n$ 是在儲存環上的每個良上的線圈數。
• $N_{i}$是每一束中的粒子數目。
• $A$ 是粒子束的截面積。

$L = f n \frac{N_{1} N_{2}}{A}$